We formalize the structure of a class of mathematical models of growing-dividing autocatalytic systems demonstrating that self-reproduction emerges only if the system's 'growth dynamics' and 'division strategy' are mutually compatible. Using various models in this class (the linear Hinshelwood cycle and nonlinear coarse-grained models of protocells and bacteria), we show that depending on the chosen division mechanism, the same chemical system can exhibit either (i) balanced exponential growth, (ii) balanced nonexponential growth, or (iii) system death (where the system either explodes to infinity or collapses to zero in successive generations). We identify the class of division processes that lead to these three outcomes, offering strategies to stabilize or destabilize growing-dividing systems. Our work provides a geometric framework to further explore growing-dividing systems and will aid in the design of self-reproducing synthetic cells.

This paper presents a multimodal dataset of 1,000 indigenous recipes from remote regions of India, collected through a participatory model involving first-time digital workers from rural areas. The project covers ten endangered language communities in six states. Documented using a dedicated mobile app, the data set includes text, images, and audio, capturing traditional food practices along with their ecological and cultural contexts. This initiative addresses gaps in food computing, such as the lack of culturally inclusive, multimodal, and community-authored data. By documenting food as it is practiced rather than prescribed, this work advances inclusive, ethical, and scalable approaches to AI-driven food systems and opens new directions in cultural AI, public health, and sustainable agriculture.

Recent developments in self-supervised learning (SSL) have made it possible to learn data representations without the need for annotations. Inspired by the non-contrastive SSL approach (SimSiam), we introduce a novel framework SIMSAM to compute the Semantic Affinity Matrix, which is significant for unsupervised image segmentation. Given an image, SIMSAM first extracts features using pre-trained DINO-ViT, then projects the features to predict the correlations of dense features in a non-contrastive way. We show applications of the Semantic Affinity Matrix in object segmentation and semantic segmentation tasks. Our code is available at this https URL.

Feature selection (FS) is assumed to improve predictive performance and identify meaningful features in high-dimensional datasets. Surprisingly, small random subsets of features (0.02-1%) match or outperform the predictive performance of both full feature sets and FS across 28 out of 30 diverse datasets (microarray, bulk and single-cell RNA-Seq, mass spectrometry, imaging, etc.). In short, any arbitrary set of features is as good as any other (with surprisingly low variance in results) - so how can a particular set of selected features be "important" if they perform no better than an arbitrary set? These results challenge the assumption that computationally selected features reliably capture meaningful signals, emphasizing the importance of rigorous validation before interpreting selected features as actionable, particularly in computational genomics.

We address the classical problem of constructing confidence intervals (CIs) for the mean of a distribution, given $N$ i.i.d. samples, such that the CI contains the true mean with probability at least $1 - \delta$, where $\delta \in (0,1)$. We characterize three distinct learning regimes based on the minimum achievable limiting width of any CI as the sample size $N_{\delta} \to \infty$ and $\delta \to 0$. In the first regime, where $N_{\delta}$ grows slower than $\log(1/\delta)$, the limiting width of any CI equals the width of the distribution's support, precluding meaningful inference. In the second regime, where $N_{\delta}$ scales as $\log(1/\delta)$, we precisely characterize the minimum limiting width, which depends on the scaling constant. In the third regime, where $N_{\delta}$ grows faster than $\log(1/\delta)$, complete learning is achievable, and the limiting width of the CI collapses to zero, converging to the true mean. We demonstrate that CIs derived from concentration inequalities based on Kullback--Leibler (KL) divergences achieve asymptotically optimal performance, attaining the minimum limiting width in both sufficient and complete learning regimes for distributions in two families: single-parameter exponential and bounded support. Additionally, these results extend to one-sided CIs, with the width notion adjusted appropriately. Finally, we generalize our findings to settings with random per-sample costs, motivated by practical applications such as stochastic simulators and cloud service selection. Instead of a fixed sample size, we consider a cost budget $C_{\delta}$, identifying analogous learning regimes and characterizing the optimal CI construction policy.

This paper presents COT-AD, a comprehensive Dataset designed to enhance cotton crop analysis through computer vision. Comprising over 25,000 images captured throughout the cotton growth cycle, with 5,000 annotated images, COT-AD includes aerial imagery for field-scale detection and segmentation and high-resolution DSLR images documenting key diseases. The annotations cover pest and disease recognition, vegetation, and weed analysis, addressing a critical gap in cotton-specific agricultural datasets. COT-AD supports tasks such as classification, segmentation, image restoration, enhancement, deep generative model-based cotton crop synthesis, and early disease management, advancing data-driven crop management

This note is intended to serve as a reference for conventions used in the literature on string compactifications, and how to move between them, collected in a single and easy-to-find place, using type IIB as an illustrative example. We hope it may be useful to beginners in the field and busy experts. E.g. string constructions proposed to address the moduli stabilisation problem are generically in regions of parameter space at the boundaries of control, so that consistent use of $2\pi$'s and frame conventions can be pivotal when computing their potentially dangerous corrections.

We investigate a geometric generalization of trifference, a concept introduced by Elias in 1988 in the study of zero-error channel capacity. In the discrete setting, a code C \subseteq {0,1,2}^n is trifferent if for any three distinct codewords x, y, z in C, there exists a coordinate i in [n] where x_i, y_i, z_i are all distinct. Determining the maximum size of such codes remains a central open problem; the classical upper bound |C| \leq 2 * (3/2)^n, proved via a simple pruning argument, has resisted significant improvement. Motivated by the search for new techniques, and in line with vectorial extensions of other classical combinatorial notions, we introduce the concept of vector trifferent codes. Consider C \subseteq (S^2)^n, where the alphabet is the unit sphere S^2 = { v in R^3 : ||v|| = 1 }. We say C is vector trifferent if for any three distinct x, y, z in C, there is an index i where the vectors x_i, y_i, z_i are mutually orthogonal. A direct reduction of the vectorial problem to the discrete setting appears infeasible, making it difficult to replicate Elias's pruning argument. Nevertheless, we develop a new method to establish the upper bound |C| \leq (sqrt(2) + o(1)) * (3/2)^n. Interestingly, our approach, when adapted back to the discrete setting, yields a polynomial improvement to Elias's bound: |C| \lesssim n^(-1/4) * (3/2)^n. This improvement arises from a technique that parallels, but is not identical to, a recent method of the authors, though it still falls short of the sharper n^(-2/5) factor obtained there. We also generalize the concept of vector trifferent codes to richer alphabets and prove a vectorial version of the Fredman-Komlos theorem (1984) for general k-separating codes.

Dynamical quantum phase transitions (DQPTs) are a class of non-equilibrium phase transitions that occur in many-body quantum systems during real-time evolution, rather than through parameter tuning as in conventional phase transitions. This paper presents an exact analytical approach to studying DQPTs by combining complex dynamics with the real-space renormalization group (RG). RG transformations are interpreted as iterated maps on the complex plane, establishing a connection between DQPTs and the Julia set, the fractal boundary separating the basins of attraction of the stable fixed points. This framework is applied to a quantum quench in the one-dimensional transverse field Ising model, and the sensitivity of DQPTs to changes in boundary conditions is examined. In particular, it is demonstrated how the topology of the spin chain influences the occurrence of DQPTs. Additionally, aqualitative argument based on quantum speed limits is provided to explain the suppression of DQPTs under certain boundary modifications.

We study the magneto-rotational instability (MRI) driven dynamo in a geometrically thin disc ($H/R\ll 1$) using stratified zero net flux (ZNF) shearing box simulations. We find that mean fields and EMFs oscillate with a primary frequency $f_{\rm dyn} = 0.017$ ($\approx 9$ orbital period), but also have higher harmonics at $3f_{\rm dyn}$. Correspondingly, the current helicity, has two frequencies $2f_{\rm dyn}$ and $4f_{\rm dyn}$ respectively, which appear to be the beat frequencies of mean fields and EMFs as expected from the magnetic helicity density evolution equation. Further, we adopt a novel inversion algorithm called the `Iterative Removal Of Sources' (IROS), to extract the turbulent dynamo coefficients in the mean-field closure using the mean magnetic fields and EMFs obtained from the shearing box simulation. We show that an $\alpha-$effect ($\alpha_{yy}$) is predominantly responsible for the creation of the poloidal field from the toroidal field, while shear generates back a toroidal field from the poloidal field; indicating that an $\alpha-\Omega$-type dynamo is operative in MRI-driven accretion discs. We also find that both strong outflow ($\bar{v}_z$) and turbulent pumping ($\gamma_z$ ) transport mean fields away from the mid-plane. Instead of turbulent diffusivity, they are the principal sink terms in the mean magnetic energy evolution equation. We find encouraging evidence that a generative helicity flux is responsible for the effective $\alpha$-effect. Finally, we point out potential limitations of horizontal ($x-y$) averaging in defining the `mean' on the extraction of dynamo coefficients and their physical interpretations.

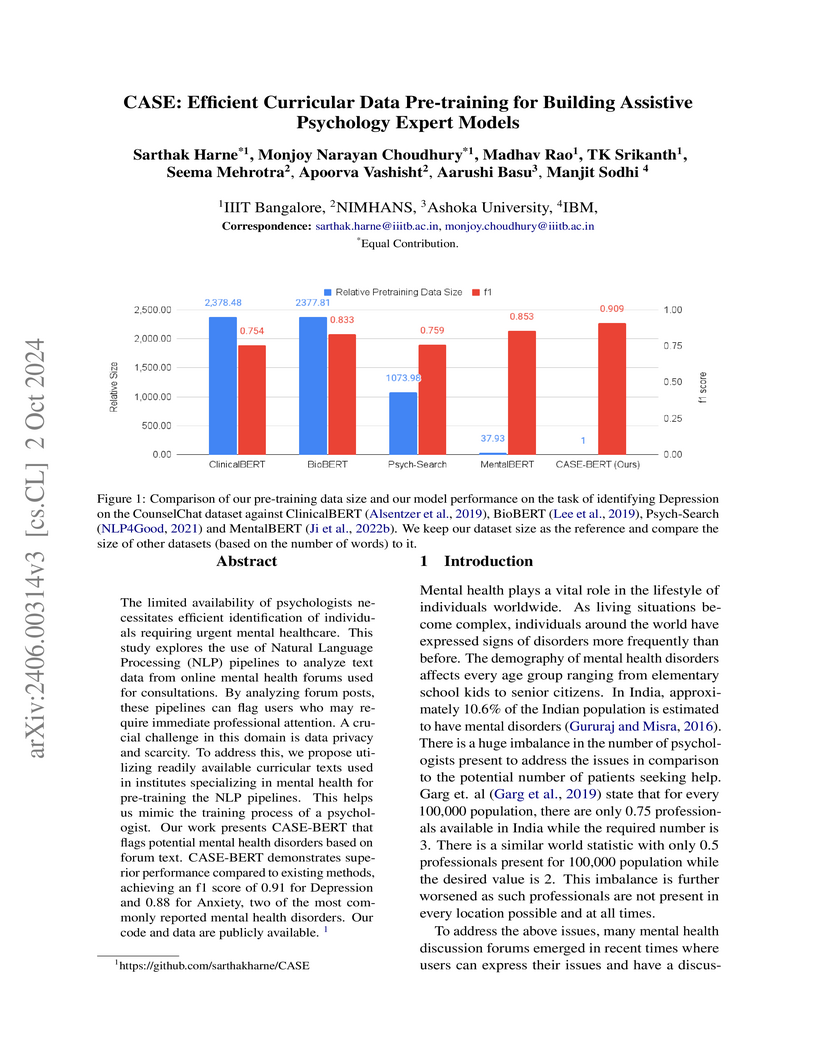
The limited availability of psychologists necessitates efficient identification of individuals requiring urgent mental healthcare. This study explores the use of Natural Language Processing (NLP) pipelines to analyze text data from online mental health forums used for consultations. By analyzing forum posts, these pipelines can flag users who may require immediate professional attention. A crucial challenge in this domain is data privacy and scarcity. To address this, we propose utilizing readily available curricular texts used in institutes specializing in mental health for pre-training the NLP pipelines. This helps us mimic the training process of a psychologist. Our work presents CASE-BERT that flags potential mental health disorders based on forum text. CASE-BERT demonstrates superior performance compared to existing methods, achieving an f1 score of 0.91 for Depression and 0.88 for Anxiety, two of the most commonly reported mental health disorders. Our code and data are publicly available.

Topic modeling has emerged as a dominant method for exploring large document collections. Recent approaches to topic modeling use large contextualized language models and variational autoencoders. In this paper, we propose a negative sampling mechanism for a contextualized topic model to improve the quality of the generated topics. In particular, during model training, we perturb the generated document-topic vector and use a triplet loss to encourage the document reconstructed from the correct document-topic vector to be similar to the input document and dissimilar to the document reconstructed from the perturbed vector. Experiments for different topic counts on three publicly available benchmark datasets show that in most cases, our approach leads to an increase in topic coherence over that of the baselines. Our model also achieves very high topic diversity.

Novice programmers frequently adopt a syntax-specific and test-case-driven approach, writing code first and adjusting until programs compile and test cases pass, rather than developing correct solutions through systematic reasoning. AI coding tools exacerbate this challenge by providing syntactically correct but conceptually flawed solutions. In this paper, we introduce BOOP (Blueprint, Operations, OCaml, Proof), a structured framework requiring four mandatory phases: formal specification, language-agnostic algorithm development, implementation, and correctness proof. This shifts focus from ``making code work'' to understanding why code is correct. BOOP was implemented at our institution using a VS Code extension and preprocessor that enforces constraints and identifies counterproductive patterns. Initial evaluation shows improved algorithmic reasoning and reduced trial-and-error debugging. Students reported better edge case understanding and problem decomposition, though some initially found the format verbose. Instructors observed stronger foundational skills compared to traditional approaches.

The importance of molecular-scale forces in sculpting biological form and function has been acknowledged for more than a century. Accounting for forces in biology is a problem that lies at the intersection of soft condensed matter physics, statistical mechanics, computer simulations and novel experimental methodologies, all adapted to a cellular context. This review surveys how forces arise within the cell. We provide a summary of the relevant background in basic biophysics, of soft-matter systems in and out of thermodynamic equilibrium, and of various force measurement methods in biology. We then show how these ideas can be incorporated into a description of cell-scale processes where forces are involved. Our examples include polymerization forces, motion of molecular motors, the properties of the actomyosin cortex, the mechanics of cell division, and shape changes in tissues. We show how new conceptual frameworks are required for understanding the consequences of cell-scale forces for biological function. We emphasize active matter descriptions, methodological tools that provide ways of incorporating non-equilibrium effects in a systematic manner into conceptual as well as quantitative descriptions. Understanding the functions of cells will necessarily require integrating the role of physical forces with the assimilation and processing of information. This integration is likely to have been a significant driver of evolutionary change.

In this paper we propose a score of an image to use for coreset selection in image classification and semantic segmentation tasks. The score is the entropy of an image as approximated by the bits-per-pixel of its compressed version. Thus the score is intrinsic to an image and does not require supervision or training. It is very simple to compute and readily available as all images are stored in a compressed format. The motivation behind our choice of score is that most other scores proposed in literature are expensive to compute. More importantly, we want a score that captures the perceptual complexity of an image. Entropy is one such measure, images with clutter tend to have a higher entropy. However sampling only low entropy iconic images, for example, leads to biased learning and an overall decrease in test performance with current deep learning models. To mitigate the bias we use a graph based method that increases the spatial diversity of the selected samples. We show that this simple score yields good results, particularly for semantic segmentation tasks.

The main goal of this article is to generalize Mess' work and using results from Labourie--Wentworth, Potrie--Sambarino and Smilga, to show that inside Hitchin representations, infinitesimal deformations of Fuchsian representations of a cocompact surface group do not act properly along the directions corresponding to the sum of a mixed odd differential and a $2m$-differential for any $1\leq m \leq \lfloor\frac{n}{2}\rfloor$. In the process, we introduce affine versions of cross ratios and triple ratios. We introduce Margulis invariants and relate them with affine crossratios and infinitesimal Jordan projections. We obtain a general equivalent criterion for existence of proper affine actions in terms of the structure of the Margulis invariant spectra. Also, using a stability argument we show the existence of proper affine actions of non-abelian free groups whose linear part is a Hitchin representation.

This paper presents a framework for developing a live vision-correcting display (VCD) to address refractive visual aberrations without the need for traditional vision correction devices like glasses or contact lenses, particularly in scenarios where wearing them may be inconvenient. We achieve this correction through deconvolution of the displayed image using a point spread function (PSF) associated with the viewer's eye. We address ringing artefacts using a masking technique applied to the prefiltered image. We also enhance the display's contrast and reduce color distortion by operating in the YUV/YCbCr color space, where deconvolution is performed solely on the luma (brightness) channel. Finally, we introduce a technique to calculate a real-time PSF that adapts based on the viewer's spherical coordinates relative to the screen. This ensures that the PSF remains accurate and undistorted even when the viewer observes the display from an angle relative to the screen normal, thereby providing consistent visual correction regardless of the viewing angle. The results of our display demonstrate significant improvements in visual clarity, achieving a structural similarity index (SSIM) of 83.04%, highlighting the effectiveness of our approach.

In this paper, we present a short proof of the limit of free energy of spherical 2 spin Sherrington-Kirkpatrick (SSK) model without external field. This proof works for all temperatures and is based on the Laplace method of integration and considering a discrete approximation of the whole space. This proof is general enough and can be adapted to any interaction matrix where the eigenvalue distribution has some nice properties. The proof in the high-temperature case is the same as the proof given in [BK19]. However, the low-temperature case is new.