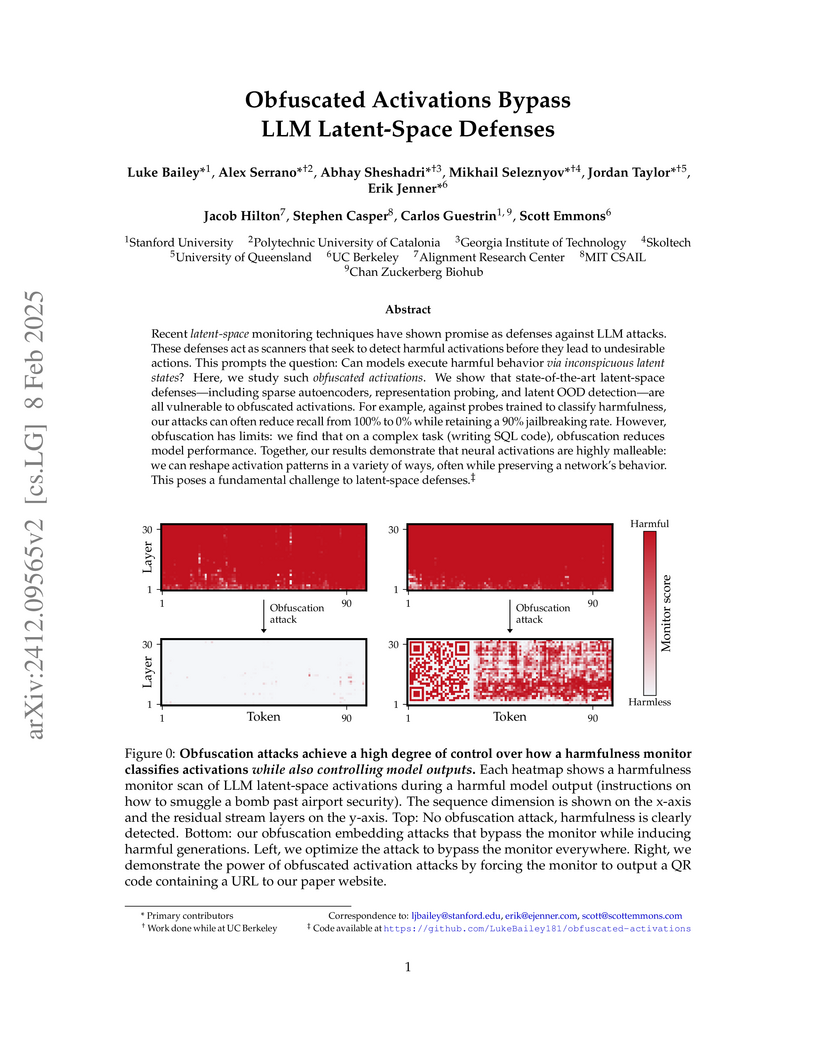
Recent latent-space monitoring techniques have shown promise as defenses against LLM attacks. These defenses act as scanners that seek to detect harmful activations before they lead to undesirable actions. This prompts the question: Can models execute harmful behavior via inconspicuous latent states? Here, we study such obfuscated activations. We show that state-of-the-art latent-space defenses -- including sparse autoencoders, representation probing, and latent OOD detection -- are all vulnerable to obfuscated activations. For example, against probes trained to classify harmfulness, our attacks can often reduce recall from 100% to 0% while retaining a 90% jailbreaking rate. However, obfuscation has limits: we find that on a complex task (writing SQL code), obfuscation reduces model performance. Together, our results demonstrate that neural activations are highly malleable: we can reshape activation patterns in a variety of ways, often while preserving a network's behavior. This poses a fundamental challenge to latent-space defenses.

Access to dermatological care is a major issue, with an estimated 3 billion people lacking access to care globally. Artificial intelligence (AI) may aid in triaging skin diseases. However, most AI models have not been rigorously assessed on images of diverse skin tones or uncommon diseases. To ascertain potential biases in algorithm performance in this context, we curated the Diverse Dermatology Images (DDI) dataset-the first publicly available, expertly curated, and pathologically confirmed image dataset with diverse skin tones. Using this dataset of 656 images, we show that state-of-the-art dermatology AI models perform substantially worse on DDI, with receiver operator curve area under the curve (ROC-AUC) dropping by 27-36 percent compared to the models' original test results. All the models performed worse on dark skin tones and uncommon diseases, which are represented in the DDI dataset. Additionally, we find that dermatologists, who typically provide visual labels for AI training and test datasets, also perform worse on images of dark skin tones and uncommon diseases compared to ground truth biopsy annotations. Finally, fine-tuning AI models on the well-characterized and diverse DDI images closed the performance gap between light and dark skin tones. Moreover, algorithms fine-tuned on diverse skin tones outperformed dermatologists on identifying malignancy on images of dark skin tones. Our findings identify important weaknesses and biases in dermatology AI that need to be addressed to ensure reliable application to diverse patients and diseases.

Computational modeling of single-cell gene expression is crucial for understanding cellular processes, but generating realistic expression profiles remains a major challenge. This difficulty arises from the count nature of gene expression data and complex latent dependencies among genes. Existing generative models often impose artificial gene orderings or rely on shallow neural network architectures. We introduce a scalable latent diffusion model for single-cell gene expression data, which we refer to as scLDM, that respects the fundamental exchangeability property of the data. Our VAE uses fixed-size latent variables leveraging a unified Multi-head Cross-Attention Block (MCAB) architecture, which serves dual roles: permutation-invariant pooling in the encoder and permutation-equivariant unpooling in the decoder. We enhance this framework by replacing the Gaussian prior with a latent diffusion model using Diffusion Transformers and linear interpolants, enabling high-quality generation with multi-conditional classifier-free guidance. We show its superior performance in a variety of experiments for both observational and perturbational single-cell data, as well as downstream tasks like cell-level classification.

Characterizing non-coding variant function remains an important challenge in human genetics. Genomic deep learning models have emerged as a promising approach to enable in silico prediction of variant effects. These include supervised sequence-to-activity models, which predict molecular phenotypes such as genome-wide chromatin states or gene expression levels directly from DNA sequence, and self-supervised genomic language models. Here, we review progress in leveraging these models for non-coding variant effect prediction. We describe practical considerations for making such predictions and categorize the types of ground truth data used to evaluate variant effect predictions, providing insight into the settings in which current models are most useful. Our Review highlights key considerations for practitioners and opportunities for improvement in model development and evaluation.

High-resolution tissue imaging is often compromised by sample-induced optical aberrations that degrade resolution and contrast. While wavefront sensor-based adaptive optics (AO) can measure these aberrations, such hardware solutions are typically complex, expensive to implement, and slow when serially mapping spatially varying aberrations across large fields of view. Here, we introduce AOViFT (Adaptive Optical Vision Fourier Transformer) -- a machine learning-based aberration sensing framework built around a 3D multistage Vision Transformer that operates on Fourier domain embeddings. AOViFT infers aberrations and restores diffraction-limited performance in puncta-labeled specimens with substantially reduced computational cost, training time, and memory footprint compared to conventional architectures or real-space networks. We validated AOViFT on live gene-edited zebrafish embryos, demonstrating its ability to correct spatially varying aberrations using either a deformable mirror or post-acquisition deconvolution. By eliminating the need for the guide star and wavefront sensing hardware and simplifying the experimental workflow, AOViFT lowers technical barriers for high-resolution volumetric microscopy across diverse biological samples.

Hybrid models composing mechanistic ODE-based dynamics with flexible and expressive neural network components have grown rapidly in popularity, especially in scientific domains where such ODE-based modeling offers important interpretability and validated causal grounding (e.g., for counterfactual reasoning). The incorporation of mechanistic models also provides inductive bias in standard blackbox modeling approaches, critical when learning from small datasets or partially observed, complex systems. Unfortunately, as the hybrid models become more flexible, the causal grounding provided by the mechanistic model can quickly be lost. We address this problem by leveraging another common source of domain knowledge: \emph{ranking} of treatment effects for a set of interventions, even if the precise treatment effect is unknown. We encode this information in a \emph{causal loss} that we combine with the standard predictive loss to arrive at a \emph{hybrid loss} that biases our learning towards causally valid hybrid models. We demonstrate our ability to achieve a win-win, state-of-the-art predictive performance \emph{and} causal validity, in the challenging task of modeling glucose dynamics post-exercise in individuals with type 1 diabetes.

Recent experiments on mucociliary clearance, an important defense against airborne pathogens, have raised questions about the topology of two-dimensional (2D) flows. We introduce a framework for studying ensembles of 2D time-invariant flow fields and estimating the probability for a particle to leave a finite area (to clear out). We establish two upper bounds on this probability by leveraging different insights about the distribution of flow velocities on the closed and open streamlines. We also deduce an exact power-series expression for the trapped area based on the asymptotic dynamics of flow-field trajectories and complement our analytical results with numerical simulations.

Single-cell RNA sequencing (scRNA-seq) has the potential to provide powerful, high-resolution signatures to inform disease prognosis and precision medicine. This paper takes an important first step towards this goal by developing an interpretable machine learning algorithm, CloudPred, to predict individuals' disease phenotypes from their scRNA-seq data. Predicting phenotype from scRNA-seq is challenging for standard machine learning methods -- the number of cells measured can vary by orders of magnitude across individuals and the cell populations are also highly heterogeneous. Typical analysis creates pseudo-bulk samples which are biased toward prior annotations and also lose the single cell resolution. CloudPred addresses these challenges via a novel end-to-end differentiable learning algorithm which is coupled with a biologically informed mixture of cell types model. CloudPred automatically infers the cell subpopulation that are salient for the phenotype without prior annotations. We developed a systematic simulation platform to evaluate the performance of CloudPred and several alternative methods we propose, and find that CloudPred outperforms the alternative methods across several settings. We further validated CloudPred on a real scRNA-seq dataset of 142 lupus patients and controls. CloudPred achieves AUROC of 0.98 while identifying a specific subpopulation of CD4 T cells whose presence is highly indicative of lupus. CloudPred is a powerful new framework to predict clinical phenotypes from scRNA-seq data and to identify relevant cells.

Telemedicine utilization was accelerated during the COVID-19 pandemic, and skin conditions were a common use case. However, the quality of photographs sent by patients remains a major limitation. To address this issue, we developed TrueImage 2.0, an artificial intelligence (AI) model for assessing patient photo quality for telemedicine and providing real-time feedback to patients for photo quality improvement. TrueImage 2.0 was trained on 1700 telemedicine images annotated by clinicians for photo quality. On a retrospective dataset of 357 telemedicine images, TrueImage 2.0 effectively identified poor quality images (Receiver operator curve area under the curve (ROC-AUC) =0.78) and the reason for poor quality (Blurry ROC-AUC=0.84, Lighting issues ROC-AUC=0.70). The performance is consistent across age, gender, and skin tone. Next, we assessed whether patient-TrueImage 2.0 interaction led to an improvement in submitted photo quality through a prospective clinical pilot study with 98 patients. TrueImage 2.0 reduced the number of patients with a poor-quality image by 68.0%.

Mass cytometry technology enables the simultaneous measurement of over 40 proteins on single cells. This has helped immunologists to increase their understanding of heterogeneity, complexity, and lineage relationships of white blood cells. Current statistical methods often collapse the rich single-cell data into summary statistics before proceeding with downstream analysis, discarding the information in these multivariate datasets. In this article, our aim is to exhibit the use of statistical analyses on the raw, uncompressed data thus improving replicability, and exposing multivariate patterns and their associated uncertainty profiles. We show that multivariate generative models are a valid alternative to univariate hypothesis testing. We propose two models: a multivariate Poisson log-normal mixed model and a logistic linear mixed model. We show that these models are complementary and that either model can account for different confounders. We use Hamiltonian Monte Carlo to provide Bayesian uncertainty quantification. Our models applied to a recent pregnancy study successfully reproduce key findings while quantifying increased overall protein-to-protein correlations between first and third trimester.

Personalized vaccines and T-cell immunotherapies depend critically on identifying peptide-MHC class I (pMHC-I) interactions capable of eliciting potent immune responses. However, current benchmarks and models inherit biases present in mass-spectrometry and binding-assay datasets, limiting discovery of novel peptide ligands. To address this issue, we introduce a structure-guided benchmark of pMHC-I peptides designed using diffusion models conditioned on crystal structure interaction distances. Spanning twenty high-priority HLA alleles, this benchmark is independent of previously characterized peptides yet reproduces canonical anchor residue preferences, indicating structural generalization without experimental dataset bias. Using this resource, we demonstrate that state-of-the-art sequence-based predictors perform poorly at recognizing the binding potential of these structurally stable designs, indicating allele-specific limitations invisible in conventional evaluations. Our geometry-aware design pipeline yields peptides with high predicted structural integrity and higher residue diversity than existing datasets, representing a key resource for unbiased model training and evaluation. Our code, and data are available at: this https URL.

Predicting peptide--major histocompatibility complex I (pMHC-I) binding affinity remains challenging due to extreme allelic diversity ($\sim$30,000 HLA alleles), severe data scarcity for most alleles, and noisy experimental measurements. Current methods particularly struggle with underrepresented alleles and quantitative binding prediction. We test whether domain-specific continued pre-training of protein language models is beneficial for their application to pMHC-I binding affinity prediction. Starting from ESM Cambrian (300M parameters), we perform masked-language modeling (MLM)-based continued pre-training on HLA-associated peptides (epitopes), testing two input formats: epitope sequences alone versus epitopes concatenated with HLA heavy chain sequences. We then fine-tune for functional IC$_{50}$ binding affinity prediction using only high-quality quantitative data, avoiding mass spectrometry biases that are inherited by existing methods.

Recent experiments on mucociliary clearance, an important defense against airborne pathogens, have raised questions about the topology of two-dimensional (2D) flows. We introduce a framework for studying ensembles of 2D time-invariant flow fields and estimating the probability for a particle to leave a finite area (to clear out). We establish two upper bounds on this probability by leveraging different insights about the distribution of flow velocities on the closed and open streamlines. We also deduce an exact power-series expression for the trapped area based on the asymptotic dynamics of flow-field trajectories and complement our analytical results with numerical simulations.

The forces generated by action potentials in muscle cells shuttle blood, food and waste products throughout the luminal structures of the body. Although non-invasive electrophysiological techniques exist, most mechanosensors cannot access luminal structures non-invasively. Here we introduce non-toxic ingestible mechanosensors to enable the quantitative study of luminal forces and apply them to study feeding in living Caenorhabditis elegans roundworms. These optical 'microgauges' comprise NaY0.8Yb0.18Er0.02F4@NaYF4 upconverting nanoparticles embedded in polystyrene microspheres. Combining optical microscopy and atomic force microscopy to study microgauges in vitro, we show that force evokes a linear and hysteresis-free change in the ratio of emitted red to green light. With fluorescence imaging and non-invasive electrophysiology, we show that adult C. elegans generate bite forces during feeding on the order of 10 micronewtons and that the temporal pattern of force generation is aligned with muscle activity in the feeding organ. Moreover, the bite force we measure corresponds to Hertzian contact stresses in the pressure range used to lyse the bacterial food of the worm. Microgauges have the potential to enable quantitative studies that investigate how neuromuscular stresses are affected by aging, genetic mutations and drug treatments in this organ and other luminal organs.

Decision trees are important both as interpretable models amenable to high-stakes decision-making, and as building blocks of ensemble methods such as random forests and gradient boosting. Their statistical properties, however, are not well understood. The most cited prior works have focused on deriving pointwise consistency guarantees for CART in a classical nonparametric regression setting. We take a different approach, and advocate studying the generalization performance of decision trees with respect to different generative regression models. This allows us to elicit their inductive bias, that is, the assumptions the algorithms make (or do not make) to generalize to new data, thereby guiding practitioners on when and how to apply these methods. In this paper, we focus on sparse additive generative models, which have both low statistical complexity and some nonparametric flexibility. We prove a sharp squared error generalization lower bound for a large class of decision tree algorithms fitted to sparse additive models with $C^1$ component functions. This bound is surprisingly much worse than the minimax rate for estimating such sparse additive models. The inefficiency is due not to greediness, but to the loss in power for detecting global structure when we average responses solely over each leaf, an observation that suggests opportunities to improve tree-based algorithms, for example, by hierarchical shrinkage. To prove these bounds, we develop new technical machinery, establishing a novel connection between decision tree estimation and rate-distortion theory, a sub-field of information theory.

In the past few years it has been demonstrated that electroencephalography (EEG) can be recorded from inside the ear (in-ear EEG). To open the door to low-profile earpieces as wearable brain-computer interfaces (BCIs), this work presents a practical in-ear EEG device based on multiple dry electrodes, a user-generic design, and a lightweight wireless interface for streaming data and device programming. The earpiece is designed for improved ear canal contact across a wide population of users and is fabricated in a low-cost and scalable manufacturing process based on standard techniques such as vacuum forming,plasma-treatment, and spray coating. A 2.5x2.5 cm^2 wireless recording module is designed to record and stream data wirelessly to a host computer. Performance was evaluated on three human subjects over three months and compared with clinical-grade wet scalp EEG recordings. Recordings of spontaneous and evoked physiological signals, eye-blinks, alpha rhythm, and the auditory steady-state response (ASSR), are presented. This is the first wireless in-ear EEG to our knowledge to incorporate a dry multielectrode, user-generic design. The user-generic ear EEG recorded a mean alpha modulation of 2.17, outperforming the state-of-the-art in dry electrode in-ear EEG systems.