With the technological advances in machine learning, effective ways are available to process the huge amount of data generated in real life. However, issues of privacy and scalability will constrain the development of machine learning. Federated learning (FL) can prevent privacy leakage by assigning training tasks to multiple clients, thus separating the central server from the local devices. However, FL still suffers from shortcomings such as single-point-failure and malicious data. The emergence of blockchain provides a secure and efficient solution for the deployment of FL. In this paper, we conduct a comprehensive survey of the literature on blockchained FL (BCFL). First, we investigate how blockchain can be applied to federal learning from the perspective of system composition. Then, we analyze the concrete functions of BCFL from the perspective of mechanism design and illustrate what problems blockchain addresses specifically for FL. We also survey the applications of BCFL in reality. Finally, we discuss some challenges and future research directions.

Open systems with gain and loss, described by non-trace-preserving, non-Hermitian Hamiltonians, have been a subject of intense research recently. The effect of exceptional-point degeneracies on the dynamics of classical systems has been observed through remarkable phenomena such as the parity-time symmetry breaking transition, asymmetric mode switching, and optimal energy transfer. On the other hand, consequences of an exceptional point for quantum evolution and decoherence are hitherto unexplored. Here, we use post-selection on a three-level superconducting transmon circuit with tunable Rabi drive, dissipation, and detuning to carry out quantum state tomography of a single dissipative qubit in the vicinity of its exceptional point. Quantum state tomography reveals the PT symmetry breaking transition at zero detuning, decoherence enhancement at finite detuning, and a quantum signature of the exceptional point in the qubit relaxation state. Our observations demonstrate rich phenomena associated with non-Hermitian physics such as non-orthogonality of eigenstates in a fully quantum regime and open routes to explore and harness exceptional point degeneracies for enhanced sensing and quantum information processing.

Extracting cause and effect phrases from a sentence is an important NLP task, with numerous applications in various domains, including legal, medical, education, and scientific research. There are many unsupervised and supervised methods proposed for solving this task. Among these, unsupervised methods utilize various linguistic tools, including syntactic patterns, dependency tree, dependency relations, etc. among different sentential units for extracting the cause and effect phrases. On the other hand, the contemporary supervised methods use various deep learning based mask language models equipped with a token classification layer for extracting cause and effect phrases. Linguistic tools, specifically, dependency tree, which organizes a sentence into different semantic units have been shown to be very effective for extracting semantic pairs from a sentence, but existing supervised methods do not have any provision for utilizing such tools within their model framework. In this work, we propose DepBERT, which extends a transformer-based model by incorporating dependency tree of a sentence within the model framework. Extensive experiments over three datasets show that DepBERT is better than various state-of-the art supervised causality extraction methods.

Open quantum systems interacting with an environment exhibit dynamics described by the combination of dissipation and coherent Hamiltonian evolution. Taken together, these effects are captured by a Liouvillian superoperator. The degeneracies of the (generically non-Hermitian) Liouvillian are exceptional points, which are associated with critical dynamics as the system approaches steady state. We use a superconducting transmon circuit coupled to an engineered environment to observe two different types of Liouvillian exceptional points that arise either from the interplay of energy loss and decoherence or purely due to decoherence. By dynamically tuning the Liouvillian superoperators in real time we observe a non-Hermiticity-induced chiral state transfer. Our study motivates a new look at open quantum system dynamics from the vantage of Liouvillian exceptional points, enabling applications of non-Hermitian dynamics in the understanding and control of open quantum systems.

Intelligent vehicles (IVs) have gained worldwide attention due to their increased convenience, safety advantages, and potential commercial value. Despite predictions of commercial deployment by 2025, implementation remains limited to small-scale validation, with precise tracking controllers and motion planners being essential prerequisites for IVs. This paper reviews state-of-the-art motion planning methods for IVs, including pipeline planning and end-to-end planning methods. The study examines the selection, expansion, and optimization operations in a pipeline method, while it investigates training approaches and validation scenarios for driving tasks in end-to-end methods. Experimental platforms are reviewed to assist readers in choosing suitable training and validation strategies. A side-by-side comparison of the methods is provided to highlight their strengths and limitations, aiding system-level design choices. Current challenges and future perspectives are also discussed in this survey.

We consider the cotangent bundle T^*F_\lambda of a GL_n partial flag variety, \lambda = (\lambda_1,...,\lambda_N), |\lambda|=\sum_i\lambda_i=n, and the torus T=(C^*)^{n+1} equivariant cohomology H^*_T(T^*F_\lambda). In [MO], a Yangian module structure was introduced on \oplus_{|\lambda|=n} H^*_T(T^*F_\lambda). We identify this Yangian module structure with the Yangian module structure introduced in [GRTV]. This identifies the operators of quantum multiplication by divisors on H^*_T(T^*F_\lambda), described in [MO], with the action of the dynamical Hamiltonians from [TV2, MTV1, GRTV]. To construct these identifications we provide a formula for the stable envelope maps, associated with the partial flag varieties and introduced in [MO]. The formula is in terms of the Yangian weight functions introduced in [TV1], c.f. [TV3, TV4], in order to construct q-hypergeometric solutions of qKZ equations.

The critical temperature of an underdoped cuprate superconductor is limited by its phase stiffness $\rho$. In this Letter we argue that the dependence of $\rho$ on doping $x$ should be understood as a consequence of deleterious competition with antiferromagnetism at large electron densities, rather than as evidence for pairing of holes in the $x =0$ Mott insulator state. Our proposal is based on the observation that the correlation energy of a d-wave superconductor increases in magnitude at finite pairing wavevector when antiferromagnetic fluctuations are strong.

The endogeneity issue is fundamentally important as many empirical applications may suffer from the omission of explanatory variables, measurement error, or simultaneous causality. Recently, \cite{hllt17} propose a "Deep Instrumental Variable (IV)" framework based on deep neural networks to address endogeneity, demonstrating superior performances than existing approaches. The aim of this paper is to theoretically understand the empirical success of the Deep IV. Specifically, we consider a two-stage estimator using deep neural networks in the linear instrumental variables model. By imposing a latent structural assumption on the reduced form equation between endogenous variables and instrumental variables, the first-stage estimator can automatically capture this latent structure and converge to the optimal instruments at the minimax optimal rate, which is free of the dimension of instrumental variables and thus mitigates the curse of dimensionality. Additionally, in comparison with classical methods, due to the faster convergence rate of the first-stage estimator, the second-stage estimator has {a smaller (second order) estimation error} and requires a weaker condition on the smoothness of the optimal instruments. Given that the depth and width of the employed deep neural network are well chosen, we further show that the second-stage estimator achieves the semiparametric efficiency bound. Simulation studies on synthetic data and application to automobile market data confirm our theory.

Entanglement in the ground state of the XY model on the infinite chain can be measured by the von Neumann entropy of a block of neighboring spins. We study a double scaling limit: the size of the block is much larger then 1 but much smaller then the length of the whole chain. In this limit, the entropy of the block approaches a constant. The limiting entropy is a function of the anisotropy and of the magnetic field. The entropy reaches minima at product states and increases boundlessly at phase transitions.

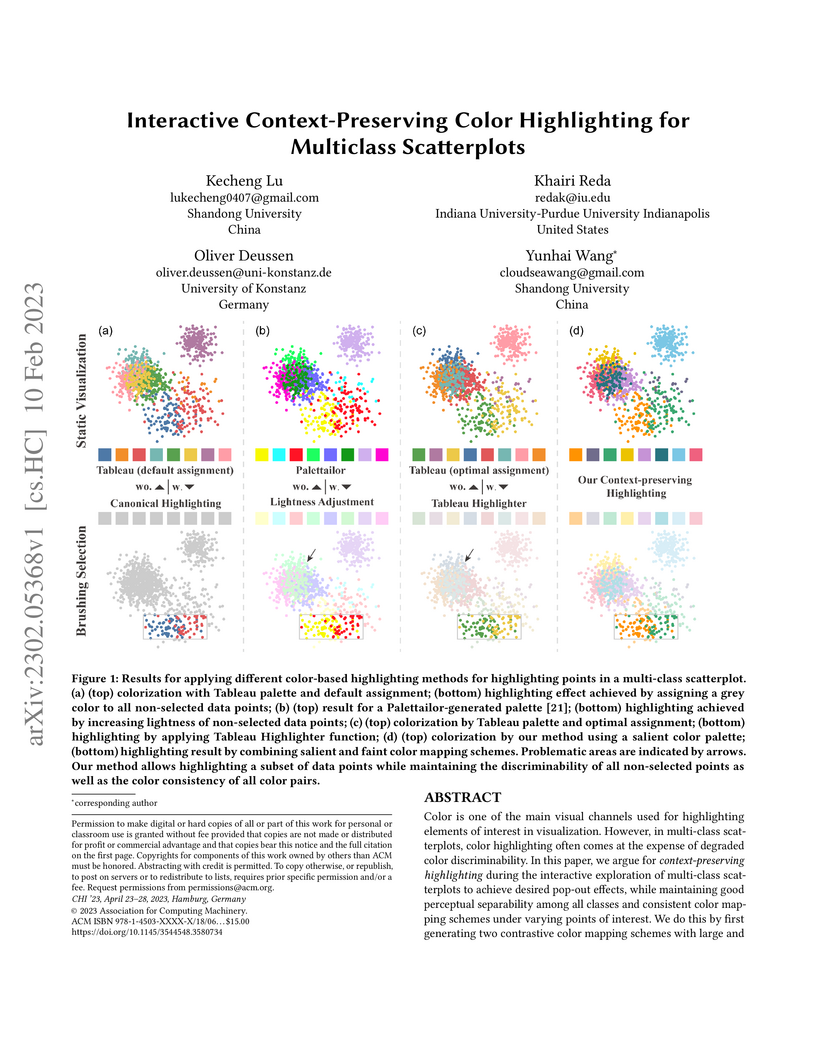
Color is one of the main visual channels used for highlighting elements of interest in visualization. However, in multi-class scatterplots, color highlighting often comes at the expense of degraded color discriminability. In this paper, we argue for context-preserving highlighting during the interactive exploration of multi-class scatterplots to achieve desired pop-out effects, while maintaining good perceptual separability among all classes and consistent color mapping schemes under varying points of interest. We do this by first generating two contrastive color mapping schemes with large and small contrasts to the background. Both schemes maintain good perceptual separability among all classes and ensure that when colors from the two palettes are assigned to the same class, they have a high color consistency in color names. We then interactively combine these two schemes to create a dynamic color mapping for highlighting different points of interest. We demonstrate the effectiveness through crowd-sourced experiments and case studies.

Conventional zero-shot learning (ZSL) methods generally learn an embedding, e.g., visual-semantic mapping, to handle the unseen visual samples via an indirect manner. In this paper, we take the advantage of generative adversarial networks (GANs) and propose a novel method, named leveraging invariant side GAN (LisGAN), which can directly generate the unseen features from random noises which are conditioned by the semantic descriptions. Specifically, we train a conditional Wasserstein GANs in which the generator synthesizes fake unseen features from noises and the discriminator distinguishes the fake from real via a minimax game. Considering that one semantic description can correspond to various synthesized visual samples, and the semantic description, figuratively, is the soul of the generated features, we introduce soul samples as the invariant side of generative zero-shot learning in this paper. A soul sample is the meta-representation of one class. It visualizes the most semantically-meaningful aspects of each sample in the same category. We regularize that each generated sample (the varying side of generative ZSL) should be close to at least one soul sample (the invariant side) which has the same class label with it. At the zero-shot recognition stage, we propose to use two classifiers, which are deployed in a cascade way, to achieve a coarse-to-fine result. Experiments on five popular benchmarks verify that our proposed approach can outperform state-of-the-art methods with significant improvements.

Recently, there have been some attempts of Transformer in 3D point cloud classification. In order to reduce computations, most existing methods focus on local spatial attention, but ignore their content and fail to establish relationships between distant but relevant points. To overcome the limitation of local spatial attention, we propose a point content-based Transformer architecture, called PointConT for short. It exploits the locality of points in the feature space (content-based), which clusters the sampled points with similar features into the same class and computes the self-attention within each class, thus enabling an effective trade-off between capturing long-range dependencies and computational complexity. We further introduce an Inception feature aggregator for point cloud classification, which uses parallel structures to aggregate high-frequency and low-frequency information in each branch separately. Extensive experiments show that our PointConT model achieves a remarkable performance on point cloud shape classification. Especially, our method exhibits 90.3% Top-1 accuracy on the hardest setting of ScanObjectNN. Source code of this paper is available at this https URL

Query similarity prediction task is generally solved by regression based models with square loss. Such a model is agnostic of absolute similarity values and it penalizes the regression error at all ranges of similarity values at the same scale. However, to boost e-commerce platform's monetization, it is important to predict high-level similarity more accurately than low-level similarity, as highly similar queries retrieves items according to user-intents, whereas moderately similar item retrieves related items, which may not lead to a purchase. Regression models fail to customize its loss function to concentrate around the high-similarity band, resulting poor performance in query similarity prediction task. We address the above challenge by considering the query prediction as an ordinal regression problem, and thereby propose a model, ORDSIM (ORDinal Regression for SIMilarity Prediction). ORDSIM exploits variable-width buckets to model ordinal loss, which penalizes errors in high-level similarity harshly, and thus enable the regression model to obtain better prediction results for high similarity values. We evaluate ORDSIM on a dataset of over 10 millions e-commerce queries from eBay platform and show that ORDSIM achieves substantially smaller prediction error compared to the competing regression methods on this dataset.

Recently, e-scooter-involved crashes have increased significantly but little information is available about the behaviors of on-road e-scooter riders. Most existing e-scooter crash research was based on retrospectively descriptive media reports, emergency room patient records, and crash reports. This paper presents a naturalistic driving study with a focus on e-scooter and vehicle encounters. The goal is to quantitatively measure the behaviors of e-scooter riders in different encounters to help facilitate crash scenario modeling, baseline behavior modeling, and the potential future development of in-vehicle mitigation algorithms. The data was collected using an instrumented vehicle and an e-scooter rider wearable system, respectively. A three-step data analysis process is developed. First, semi-automatic data labeling extracts e-scooter rider images and non-rider human images in similar environments to train an e-scooter-rider classifier. Then, a multi-step scene reconstruction pipeline generates vehicle and e-scooter trajectories in all encounters. The final step is to model e-scooter rider behaviors and e-scooter-vehicle encounter scenarios. A total of 500 vehicle to e-scooter interactions are analyzed. The variables pertaining to the same are also discussed in this paper.

We consider actions of the current Lie algebras $\mathfrak{gl}_{n}[t]$ and $\mathfrak{gl}_{k}[t]$ on the space of polynomials in $kn$ anticommuting variables. The actions depend on parameters $\bar{z}=(z_{1}\dots z_{k})$ and $\bar{\alpha}=(\alpha_{1}\dots \alpha_{n})$, respectively. We show that the images of the Bethe algebras $\mathcal{B}_{\bar{\alpha}}^{\langle n \rangle}\subset U(\mathfrak{gl}_{n}[t])$and$\mathcal{B}_{\bar{z}}^{\langle k \rangle}\subset U(\mathfrak{gl}_{k}[t])$ under these actions coincide. To prove the statement, we use the Bethe ansatz description of eigenvalues of the actions of the Bethe algebras via spaces of quasi-exponentials and establish an explicit correspondence between these spaces for the actions of $\mathcal{B}_{\bar{\alpha}}^{\langle n \rangle}$ and $\mathcal{B}_{\bar{z}}^{\langle k \rangle}$.

Partial domain adaptation aims to adapt knowledge from a larger and more diverse source domain to a smaller target domain with less number of classes, which has attracted appealing attention. Recent practice on domain adaptation manages to extract effective features by incorporating the pseudo labels for the target domain to better fight off the cross-domain distribution divergences. However, it is essential to align target data with only a small set of source data. In this paper, we develop a novel Discriminative Cross-Domain Feature Learning (DCDF) framework to iteratively optimize target labels with a cross-domain graph in a weighted scheme. Specifically, a weighted cross-domain center loss and weighted cross-domain graph propagation are proposed to couple unlabeled target data to related source samples for discriminative cross-domain feature learning, where irrelevant source centers will be ignored, to alleviate the marginal and conditional disparities simultaneously. Experimental evaluations on several popular benchmarks demonstrate the effectiveness of our proposed approach on facilitating the recognition for the unlabeled target domain, through comparing it to the state-of-the-art partial domain adaptation approaches.

One of the central goals in precision health is the understanding and interpretation of high-dimensional biological data to identify genes and markers associated with disease initiation, development, and outcomes. Though significant effort has been committed to harness gene expression data for multiple analyses while accounting for time-to-event modeling by including survival times, many traditional analyses have focused separately on non-negative matrix factorization (NMF) of the gene expression data matrix and survival regression with Cox proportional hazards model. In this work, Cox proportional hazards regression is integrated with NMF by imposing survival constraints. This is accomplished by jointly optimizing the Frobenius norm and partial log likelihood for events such as death or relapse. Simulation results on synthetic data demonstrated the superiority of the proposed method, when compared to other algorithms, in finding survival associated gene clusters. In addition, using human cancer gene expression data, the proposed technique can unravel critical clusters of cancer genes. The discovered gene clusters reflect rich biological implications and can help identify survival-related biomarkers. Towards the goal of precision health and cancer treatments, the proposed algorithm can help understand and interpret high-dimensional heterogeneous genomics data with accurate identification of survival-associated gene clusters.

Much evidence seems to suggest cortex operates near a critical point, yet a single set of exponents defining its universality class has not been found. In fact, when critical exponents are estimated from data, they widely differ across species, individuals of the same species, and even over time, or depending on stimulus. Interestingly, these exponents still approximately hold to a dynamical scaling relation. Here we show that the theory of quasicriticality, an organizing principle for brain dynamics, can account for this paradoxical situation. As external stimuli drive the cortex, quasicriticality predicts a departure from criticality along a Widom line with exponents that decrease in absolute value, while still holding approximately to a dynamical scaling relation. We use simulations and experimental data to confirm these predictions and describe new ones that could be tested soon.

We describe \,$q$-hypergeometric solutions of the equivariant quantum differential equations and associated qKZ difference equations for the cotangent bundle $T^*F_\lambda$ of a partial flag variety \,$F_\lambda$\,. These \,$q$-hypergeometric solutions manifest a Landau-Ginzburg mirror symmetry for the cotangent bundle. We formulate and prove Pieri rules for quantum equivariant cohomology of the cotangent bundle. Our Gamma theorem for \,$T^*F_\lambda$ \,says that the leading term of the asymptotics of the \,$q$-hypergeometric solutions can be written as the equivariant Gamma class of the tangent bundle of $T^*F_\lambda$ multiplied by the exponentials of the equivariant first Chern classes of the associated vector bundles. That statement is analogous to the statement of the gamma conjecture by B.\,Dubrovin and by S.\,Galkin, V.\,Golyshev, and H.\,Iritani, see also the Gamma theorem for \,$F_\lambda$ \,in Appendix B.

We investigate PT -symmetry breaking transitions in a dimer comprising two LC oscillators, one with loss and the second with gain. The electric energy of this four-mode model oscillates between the two LC circuits, and between capacitive and inductive energy within each LC circuit. Its dynamics are described by a non-Hermitian, PT -symmetric Hamiltonian with three different phases separated by two exceptional points. We systematically measure the eigenfrequencies of energy dynamics across the three regions as a function of gain-loss strength. In addition to observe the well-studied PT transition for oscillations across the two LC circuits, at higher gain-loss strength, transition within each LC circuit is also observed. With their extraordinary tuning ability, PT -symmetric electronics are ideally suited for classical simulations of non-Hermitian systems