Knowledge Graphs (KGs) are valuable tools for representing relationships between entities in a structured format. Traditionally, these knowledge bases are queried to extract specific information. However, question-answering (QA) over such KGs poses a challenge due to the intrinsic complexity of natural language compared to the structured format and the size of these graphs. Despite these challenges, the structured nature of KGs can provide a solid foundation for grounding the outputs of Large Language Models (LLMs), offering organizations increased reliability and control. Recent advancements in LLMs have introduced reasoning methods at inference time to improve their performance and maximize their capabilities. In this work, we propose integrating these reasoning strategies with KGs to anchor every step or "thought" of the reasoning chains in KG data. Specifically, we evaluate both agentic and automated search methods across several reasoning strategies, including Chain-of-Thought (CoT), Tree-of-Thought (ToT), and Graph-of-Thought (GoT), using GRBench, a benchmark dataset for graph reasoning with domain-specific graphs. Our experiments demonstrate that this approach consistently outperforms baseline models, highlighting the benefits of grounding LLM reasoning processes in structured KG data.

When designing a new API for a large project, developers need to make smart design choices so that their code base can grow sustainably. To ensure that new API components are well designed, developers can learn from existing API components. However, the lack of standardized methods for comparing API designs makes this learning process time-consuming and difficult. To address this gap we developed API-Miner, to the best of our knowledge, one of the first API-to-API specification recommendation engines. API-Miner retrieves relevant specification components written in OpenAPI (a widely adopted language used to describe web APIs). API-miner presents several significant contributions, including: (1) novel methods of processing and extracting key information from OpenAPI specifications, (2) innovative feature extraction techniques that are optimized for the highly technical API specification domain, and (3) a novel log-linear probabilistic model that combines multiple signals to retrieve relevant and high quality OpenAPI specification components given a query specification. We evaluate API-Miner in both quantitative and qualitative tasks and achieve an overall of 91.7% recall@1 and 56.2% F1, which surpasses baseline performance by 15.4% in recall@1 and 3.2% in F1. Overall, API-Miner will allow developers to retrieve relevant OpenAPI specification components from a public or internal database in the early stages of the API development cycle, so that they can learn from existing established examples and potentially identify redundancies in their work. It provides the guidance developers need to accelerate development process and contribute thoughtfully designed APIs that promote code maintainability and quality. Code is available on GitHub at this https URL

Limit Order Books (LOBs) serve as a mechanism for buyers and sellers to interact with each other in the financial markets. Modelling and simulating LOBs is quite often necessary for calibrating and fine-tuning the automated trading strategies developed in algorithmic trading research. The recent AI revolution and availability of faster and cheaper compute power has enabled the modelling and simulations to grow richer and even use modern AI techniques. In this review we examine the various kinds of LOB simulation models present in the current state of the art. We provide a classification of the models on the basis of their methodology and provide an aggregate view of the popular stylized facts used in the literature to test the models. We additionally provide a focused study of price impact's presence in the models since it is one of the more crucial phenomena to model in algorithmic trading. Finally, we conduct a comparative analysis of various qualities of fits of these models and how they perform when tested against empirical data.

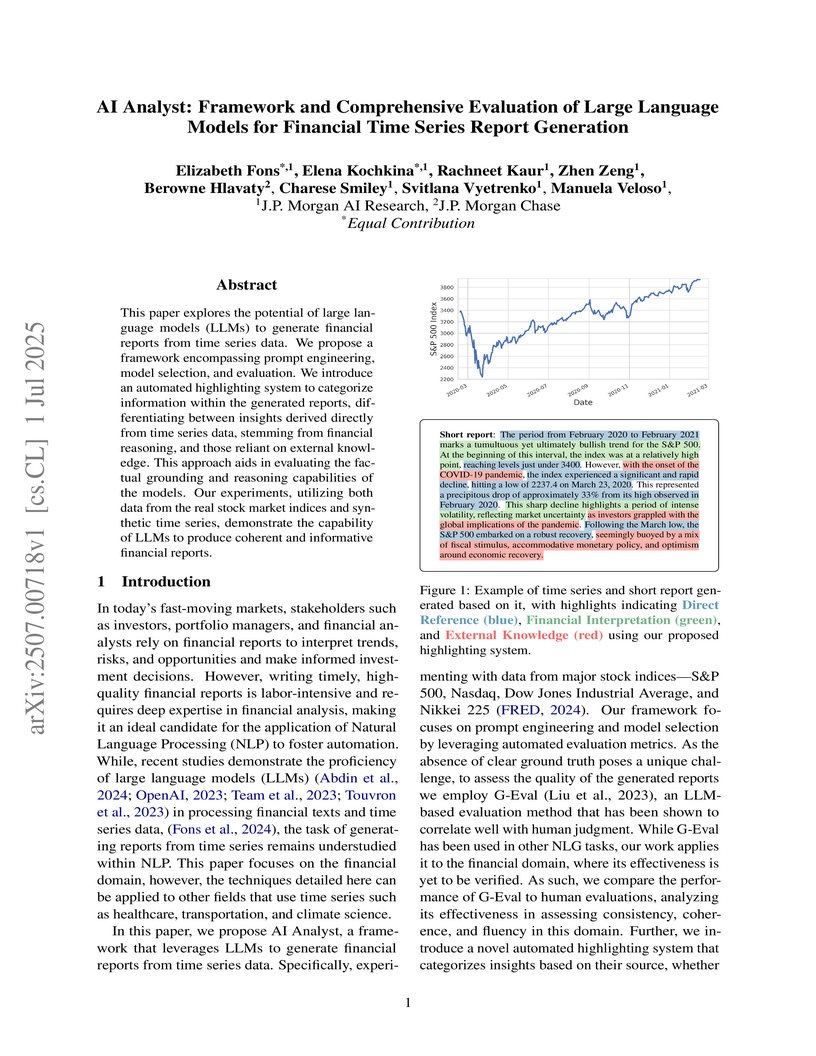
This paper explores the potential of large language models (LLMs) to generate financial reports from time series data. We propose a framework encompassing prompt engineering, model selection, and evaluation. We introduce an automated highlighting system to categorize information within the generated reports, differentiating between insights derived directly from time series data, stemming from financial reasoning, and those reliant on external knowledge. This approach aids in evaluating the factual grounding and reasoning capabilities of the models. Our experiments, utilizing both data from the real stock market indices and synthetic time series, demonstrate the capability of LLMs to produce coherent and informative financial reports.

Hawkes Process has been used to model Limit Order Book (LOB) dynamics in several ways in the literature however the focus has been limited to capturing the inter-event times while the order size is usually assumed to be constant. We propose a novel methodology of using Compound Hawkes Process for the LOB where each event has an order size sampled from a calibrated distribution. The process is formulated in a novel way such that the spread of the process always remains positive. Further, we condition the model parameters on time of day to support empirical observations. We make use of an enhanced non-parametric method to calibrate the Hawkes kernels and allow for inhibitory cross-excitation kernels. We showcase the results and quality of fits for an equity stock's LOB in the NASDAQ exchange and compare them against several baselines. Finally, we conduct a market impact study of the simulator and show the empirical observation of a concave market impact function is indeed replicated.

The advent of personalized content generation by LLMs presents a novel challenge: how to efficiently adapt text to meet individual preferences without the unsustainable demand of creating a unique model for each user. This study introduces an innovative online method that employs neural bandit algorithms to dynamically optimize soft instruction embeddings based on user feedback, enhancing the personalization of open-ended text generation by white-box LLMs. Through rigorous experimentation on various tasks, we demonstrate significant performance improvements over baseline strategies. NeuralTS, in particular, leads to substantial enhancements in personalized news headline generation, achieving up to a 62.9% improvement in terms of best ROUGE scores and up to 2.76% increase in LLM-agent evaluation against the baseline.

We present a randomized algorithm for producing a quasi-optimal hierarchically semi-separable (HSS) approximation to an $N\times N$ matrix $A$ using only matrix-vector products with $A$ and $A^T$. We prove that, using $O(k \log(N/k))$ matrix-vector products and ${O}(N k^2 \log(N/k))$ additional runtime, the algorithm returns an HSS matrix $B$ with rank-$k$ blocks whose expected Frobenius norm error $\mathbb{E}[\|A - B\|_F^2]$ is at most $O(\log(N/k))$ times worse than the best possible approximation error by an HSS rank-$k$ matrix. In fact, the algorithm we analyze in a simple modification of an empirically effective method proposed by [Levitt & Martinsson, SISC 2024]. As a stepping stone towards our main result, we prove two results that are of independent interest: a similar guarantee for a variant of the algorithm which accesses $A$'s entries directly, and explicit error bounds for near-optimal subspace approximation using projection-cost-preserving sketches. To the best of our knowledge, our analysis constitutes the first polynomial-time quasi-optimality result for HSS matrix approximation, both in the explicit access model and the matrix-vector product query model.

Financial decision-making hinges on the analysis of relevant information embedded in the enormous volume of documents in the financial domain. To address this challenge, we developed FinQAPT, an end-to-end pipeline that streamlines the identification of relevant financial reports based on a query, extracts pertinent context, and leverages Large Language Models (LLMs) to perform downstream tasks. To evaluate the pipeline, we experimented with various techniques to optimize the performance of each module using the FinQA dataset. We introduced a novel clustering-based negative sampling technique to enhance context extraction and a novel prompting method called Dynamic N-shot Prompting to boost the numerical question-answering capabilities of LLMs. At the module level, we achieved state-of-the-art accuracy on FinQA, attaining an accuracy of 80.6%. However, at the pipeline level, we observed decreased performance due to challenges in extracting relevant context from financial reports. We conducted a detailed error analysis of each module and the end-to-end pipeline, pinpointing specific challenges that must be addressed to develop a robust solution for handling complex financial tasks.

Despite the remarkable coherence of Large Language Models (LLMs), existing evaluation methods often suffer from fluency bias and rely heavily on multiple-choice formats, making it difficult to assess factual accuracy and complex reasoning effectively. LLMs thus frequently generate factually inaccurate responses, especially in complex reasoning tasks, highlighting two prominent challenges: (1) the inadequacy of existing methods to evaluate reasoning and factual accuracy effectively, and (2) the reliance on human evaluators for nuanced judgment, as illustrated by Williams and Huckle (2024)[1], who found manual grading indispensable despite automated grading advancements. To address evaluation gaps in open-ended reasoning tasks, we introduce the EQUATOR Evaluator (Evaluation of Question Answering Thoroughness in Open-ended Reasoning). This framework combines deterministic scoring with a focus on factual accuracy and robust reasoning assessment. Using a vector database, EQUATOR pairs open-ended questions with human-evaluated answers, enabling more precise and scalable evaluations. In practice, EQUATOR significantly reduces reliance on human evaluators for scoring and improves scalability compared to Williams and Huckle's (2004)[1] methods. Our results demonstrate that this framework significantly outperforms traditional multiple-choice evaluations while maintaining high accuracy standards. Additionally, we introduce an automated evaluation process leveraging smaller, locally hosted LLMs. We used LLaMA 3.2B, running on the Ollama binaries to streamline our assessments. This work establishes a new paradigm for evaluating LLM performance, emphasizing factual accuracy and reasoning ability, and provides a robust methodological foundation for future research.

A high-velocity paradigm shift towards Explainable Artificial Intelligence (XAI) has emerged in recent years. Highly complex Machine Learning (ML) models have flourished in many tasks of intelligence, and the questions have started to shift away from traditional metrics of validity towards something deeper: What is this model telling me about my data, and how is it arriving at these conclusions? Inconsistencies between XAI and modeling techniques can have the undesirable effect of casting doubt upon the efficacy of these explainability approaches. To address these problems, we propose a systematic, perturbation-based analysis against a popular, model-agnostic method in XAI, SHapley Additive exPlanations (Shap). We devise algorithms to generate relative feature importance in settings of dynamic inference amongst a suite of popular machine learning and deep learning methods, and metrics that allow us to quantify how well explanations generated under the static case hold. We propose a taxonomy for feature importance methodology, measure alignment, and observe quantifiable similarity amongst explanation models across several datasets.

Social science NLP tasks, such as emotion or humor detection, are required to capture the semantics along with the implicit pragmatics from text, often with limited amounts of training data. Instruction tuning has been shown to improve the many capabilities of large language models (LLMs) such as commonsense reasoning, reading comprehension, and computer programming. However, little is known about the effectiveness of instruction tuning on the social domain where implicit pragmatic cues are often needed to be captured. We explore the use of instruction tuning for social science NLP tasks and introduce Socialite-Llama -- an open-source, instruction-tuned Llama. On a suite of 20 social science tasks, Socialite-Llama improves upon the performance of Llama as well as matches or improves upon the performance of a state-of-the-art, multi-task finetuned model on a majority of them. Further, Socialite-Llama also leads to improvement on 5 out of 6 related social tasks as compared to Llama, suggesting instruction tuning can lead to generalized social understanding. All resources including our code, model and dataset can be found through this http URL.

Recent advancements in transformer-based speech representation models have greatly transformed speech processing. However, there has been limited research conducted on evaluating these models for speech emotion recognition (SER) across multiple languages and examining their internal representations. This article addresses these gaps by presenting a comprehensive benchmark for SER with eight speech representation models and six different languages. We conducted probing experiments to gain insights into inner workings of these models for SER. We find that using features from a single optimal layer of a speech model reduces the error rate by 32\% on average across seven datasets when compared to systems where features from all layers of speech models are used. We also achieve state-of-the-art results for German and Persian languages. Our probing results indicate that the middle layers of speech models capture the most important emotional information for speech emotion recognition.

Chest Computational Tomography (CT) scans present low cost, speed and objectivity for COVID-19 diagnosis and deep learning methods have shown great promise in assisting the analysis and interpretation of these images. Most hospitals or countries can train their own models using in-house data, however empirical evidence shows that those models perform poorly when tested on new unseen cases, surfacing the need for coordinated global collaboration. Due to privacy regulations, medical data sharing between hospitals and nations is extremely difficult. We propose a GAN-augmented federated learning model, dubbed ST-FL (Style Transfer Federated Learning), for COVID-19 image segmentation. Federated learning (FL) permits a centralised model to be learned in a secure manner from heterogeneous datasets located in disparate private data silos. We demonstrate that the widely varying data quality on FL client nodes leads to a sub-optimal centralised FL model for COVID-19 chest CT image segmentation. ST-FL is a novel FL framework that is robust in the face of highly variable data quality at client nodes. The robustness is achieved by a denoising CycleGAN model at each client of the federation that maps arbitrary quality images into the same target quality, counteracting the severe data variability evident in real-world FL use-cases. Each client is provided with the target style, which is the same for all clients, and trains their own denoiser. Our qualitative and quantitative results suggest that this FL model performs comparably to, and in some cases better than, a model that has centralised access to all the training data.

In deep learning, embeddings are widely used to represent categorical entities such as words, apps, and movies. An embedding layer maps each entity to a unique vector, causing the layer's memory requirement to be proportional to the number of entities. In the recommendation domain, a given category can have hundreds of thousands of entities, and its embedding layer can take gigabytes of memory. The scale of these networks makes them difficult to deploy in resource constrained environments. In this paper, we propose a novel approach for reducing the size of an embedding table while still mapping each entity to its own unique embedding. Rather than maintaining the full embedding table, we construct each entity's embedding "on the fly" using two separate embedding tables. The first table employs hashing to force multiple entities to share an embedding. The second table contains one trainable weight per entity, allowing the model to distinguish between entities sharing the same embedding. Since these two tables are trained jointly, the network is able to learn a unique embedding per entity, helping it maintain a discriminative capability similar to a model with an uncompressed embedding table. We call this approach MEmCom (Multi-Embedding Compression). We compare with state-of-the-art model compression techniques for multiple problem classes including classification and ranking. On four popular recommender system datasets, MEmCom had a 4% relative loss in nDCG while compressing the input embedding sizes of our recommendation models by 16x, 4x, 12x, and 40x. MEmCom outperforms the state-of-the-art techniques, which achieved 16%, 6%, 10%, and 8% relative loss in nDCG at the respective compression ratios. Additionally, MEmCom is able to compress the RankNet ranking model by 32x on a dataset with millions of users' interactions with games while incurring only a 1% relative loss in nDCG.

Code revert prediction, a specialized form of software defect detection, aims to forecast or predict the likelihood of code changes being reverted or rolled back in software development. This task is very important in practice because by identifying code changes that are more prone to being reverted, developers and project managers can proactively take measures to prevent issues, improve code quality, and optimize development processes. However, compared to code defect detection, code revert prediction has been rarely studied in previous research. Additionally, many previous methods for code defect detection relied on independent features but ignored relationships between code scripts. Moreover, new challenges are introduced due to constraints in an industry setting such as company regulation, limited features and large-scale codebase. To overcome these limitations, this paper presents a systematic empirical study for code revert prediction that integrates the code import graph with code features. Different strategies to address anomalies and data imbalance have been implemented including graph neural networks with imbalance classification and anomaly detection. We conduct the experiments on real-world code commit data within J.P. Morgan Chase which is extremely imbalanced in order to make a comprehensive comparison of these different approaches for the code revert prediction problem.

Tick-sizes not only influence the granularity of the price formation process but also affect market agents' behavior. We investigate the disparity in the microstructural properties of the Limit Order Book (LOB) across a basket of assets with different relative tick-sizes. A key contribution of this study is the identification of several stylized facts, which are used to differentiate between large, medium, and small-tick assets, along with clear metrics for their measurement. We provide cross-asset visualizations to illustrate how these attributes vary with relative tick-size. Further, we propose a Hawkes Process model that {\color{black}not only fits well for large-tick assets, but also accounts for }sparsity, multi-tick level price moves, and the shape of the LOB in small-tick assets. Through simulation studies, we demonstrate the {\color{black} versatility} of the model and identify key variables that determine whether a simulated LOB resembles a large-tick or small-tick asset. Our tests show that stylized facts like sparsity, shape, and relative returns distribution can be smoothly transitioned from a large-tick to a small-tick asset using our model. We test this model's assumptions, showcase its challenges and propose questions for further directions in this area of research.

The subject of green AI has been gaining attention within the deep learning community given the recent trend of ever larger and more complex neural network models. Existing solutions for reducing the computational load of training at inference time usually involve pruning the network parameters. Pruning schemes often create extra overhead either by iterative training and fine-tuning for static pruning or repeated computation of a dynamic pruning graph. We propose a new parameter pruning strategy for learning a lighter-weight sub-network that minimizes the energy cost while maintaining comparable performance to the fully parameterised network on given downstream tasks. Our proposed pruning scheme is green-oriented, as it only requires a one-off training to discover the optimal static sub-networks by dynamic pruning methods. The pruning scheme consists of a binary gating module and a polarizing loss function to uncover sub-networks with user-defined sparsity. Our method enables pruning and training simultaneously, which saves energy in both the training and inference phases and avoids extra computational overhead from gating modules at inference time. Our results on CIFAR-10, CIFAR-100, and Tiny Imagenet suggest that our scheme can remove 50% of connections in deep networks with <1% reduction in classification accuracy. Compared to other related pruning methods, our method demonstrates a lower drop in accuracy for equivalent reductions in computational cost.

Distributed ledger technology offers several advantages for banking and finance industry, including efficient transaction processing and cross-party transaction reconciliation. The key challenges for adoption of this technology in financial institutes are (a) the building of a privacy-preserving ledger, (b) supporting auditing and regulatory requirements, and (c) flexibility to adapt to complex use-cases with multiple digital assets and actors. This paper proposes a framework for a private, audit-able, and distributed ledger (PADL) that adapts easily to fundamental use-cases within financial institutes. PADL employs widely-used cryptography schemes combined with zero-knowledge proofs to propose a transaction scheme for a `table' like ledger. It enables fast confidential peer-to-peer multi-asset transactions, and transaction graph anonymity, in a no-trust setup, but with customized privacy. We prove that integrity and anonymity of PADL is secured against a strong threat model. Furthermore, we showcase three fundamental real-life use-cases, namely, an assets exchange ledger, a settlement ledger, and a bond market ledger. Based on these use-cases we show that PADL supports smooth-lined inter-assets auditing while preserving privacy of the participants. For example, we show how a bank can be audited for its liquidity or credit risk without violation of privacy of itself or any other party, or how can PADL ensures honest coupon rate payment in bond market without sharing investors values. Finally, our evaluation shows PADL's advantage in performance against previous relevant schemes.