Innopolis University
Optimal Flow Matching (OFM) introduces a method to learn generative flows with perfectly straight trajectories, directly recovering the optimal transport map in a single training step. The approach achieves superior performance on high-dimensional optimal transport benchmarks and competitive results in unpaired image-to-image translation while enabling efficient one-step inference.
The recently proposed Large Concept Model (LCM) generates text by predicting a sequence of sentence-level embeddings and training with either mean-squared error or diffusion objectives. We present SONAR-LLM, a decoder-only transformer that "thinks" in the same continuous SONAR embedding space, yet is supervised through token-level cross-entropy propagated via the frozen SONAR decoder. This hybrid objective retains the semantic abstraction of LCM while eliminating its diffusion sampler and restoring a likelihood-based training signal. Across model sizes from 39M to 1.3B parameters, SONAR-LLM attains competitive generation quality. We report scaling trends, ablations, benchmark results, and release the complete training code and all pretrained checkpoints to foster reproducibility and future research.
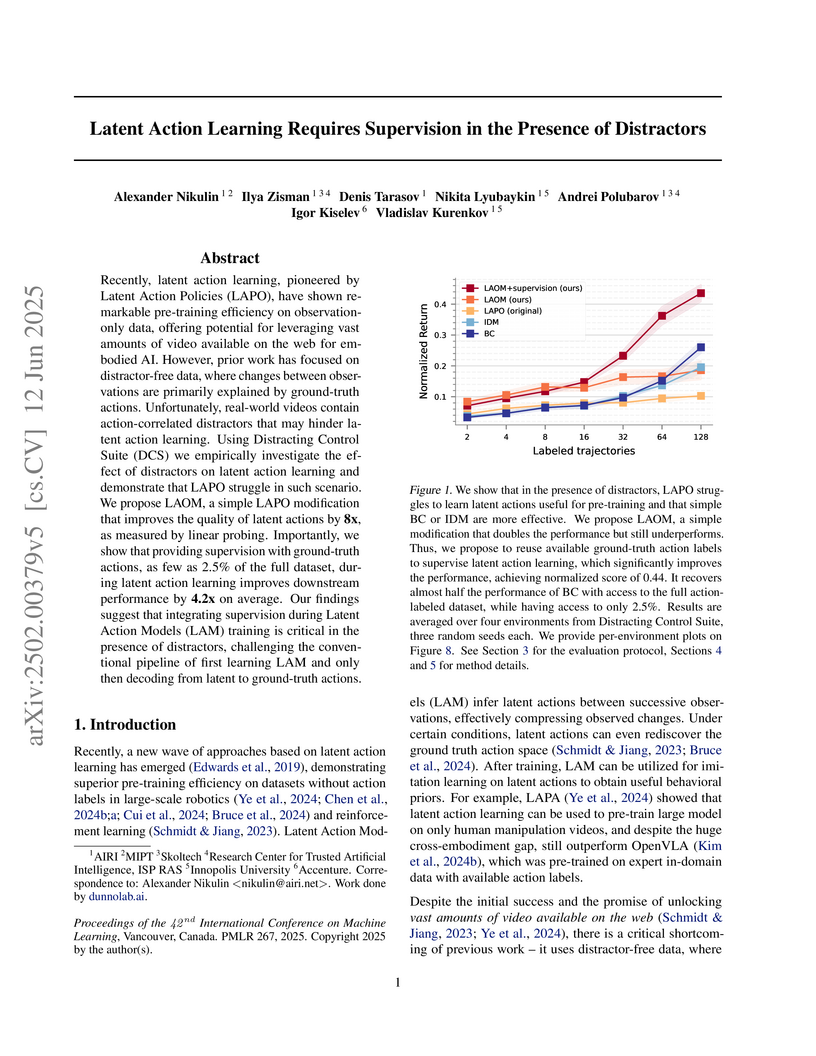
This research empirically demonstrates that latent action models struggle to learn useful actions when trained on observational data containing real-world distractors. Integrating minimal ground-truth action supervision directly into the latent action model's initial training phase improves downstream policy performance by 4.3x on average and enables better generalization to novel distractors.
A theoretical framework combines sheaf theory with causal emergence analysis to identify and measure resilient macro-structures in distributed systems, introducing a causal resilience index that quantifies how effectively higher-level system descriptions capture robust behavior compared to component-level analysis.
Chaos engineering reveals resilience risks but is expensive and operationally risky to run broadly and often. Model-based analyses can estimate dependability, yet in practice they are tricky to build and keep current because models are typically handcrafted. We claim that a simple connectivity-only topological model - just the service-dependency graph plus replica counts - can provide fast, low-risk availability estimates under fail-stop faults. To make this claim practical without hand-built models, we introduce model discovery: an automated step that can run in CI/CD or as an observability-platform capability, synthesizing an explicit, analyzable model from artifacts teams already have (e.g., distributed traces, service-mesh telemetry, configs/manifests) - providing an accessible gateway for teams to begin resilience testing. As a proof by instance on the DeathStarBench Social Network, we extract the dependency graph from Jaeger and estimate availability across two deployment modes and five failure rates. The discovered model closely tracks live fault-injection results; with replication, median error at mid-range failure rates is near zero, while no-replication shows signed biases consistent with excluded mechanisms. These results create two opportunities: first, to triage and reduce the scope of expensive chaos experiments in advance, and second, to generate real-time signals on the system's resilience posture as its topology evolves, preserving live validation for the most critical or ambiguous scenarios.
The cadrille framework introduces a multi-modal CAD reconstruction system that uses a two-stage training paradigm, including online reinforcement learning, to generate executable Python scripts from point clouds, images, and text. It achieves state-of-the-art performance across challenging benchmarks, significantly reducing the invalidity ratio to near-zero and improving reconstruction accuracy.
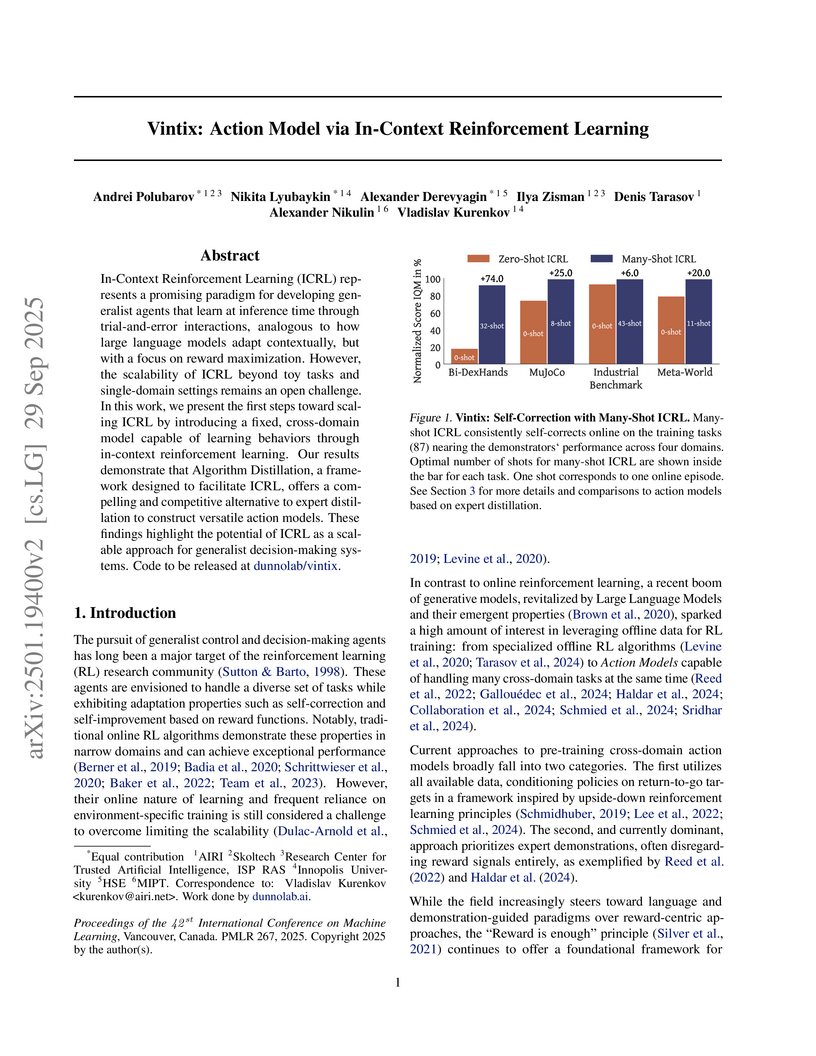
Vintix introduces a method to scale In-Context Reinforcement Learning (ICRL) for generalist agents in continuous, cross-domain control tasks. It employs a 300M-parameter Transformer model trained with Algorithm Distillation on trajectories generated by a Continuous Noise Distillation approach, demonstrating inference-time self-correction and superior performance over expert-distilled models.
16 Oct 2025
Fine-tuning Large Language Models (LLMs) is essential for adapting pre-trained models to downstream tasks. Yet traditional first-order optimizers such as Stochastic Gradient Descent (SGD) and Adam incur prohibitive memory and computational costs that scale poorly with model size. In this paper, we investigate zero-order (ZO) optimization methods as a memory- and compute-efficient alternative, particularly in the context of parameter-efficient fine-tuning techniques like LoRA. We propose JAGUAR SignSGD, a ZO momentum-based algorithm that extends ZO SignSGD, requiring the same number of parameters as the standard ZO SGD and only O(1) function evaluations per iteration. To the best of our knowledge, this is the first study to establish rigorous convergence guarantees for SignSGD in the stochastic ZO case. We further propose JAGUAR Muon, a novel ZO extension of the Muon optimizer that leverages the matrix structure of model parameters, and we provide its convergence rate under arbitrary stochastic noise. Through extensive experiments on challenging LLM fine-tuning benchmarks, we demonstrate that the proposed algorithms meet or exceed the convergence quality of standard first-order methods, achieving significant memory reduction. Our theoretical and empirical results establish new ZO optimization methods as a practical and theoretically grounded approach for resource-constrained LLM adaptation. Our code is available at this https URL
22 Oct 2025
Optimization lies at the core of modern deep learning, yet existing methods often face a fundamental trade-off between adapting to problem geometry and leveraging curvature utilization. Steepest descent algorithms adapt to different geometries through norm choices but remain strictly first-order, whereas quasi-Newton and adaptive optimizers incorporate curvature information but are restricted to Frobenius geometry, limiting their applicability across diverse architectures. In this work, we propose a unified framework generalizing steepest descent, quasi-Newton methods, and adaptive methods through the novel notion of preconditioned matrix norms. This abstraction reveals that widely used optimizers such as SGD and Adam, as well as more advanced approaches like Muon and KL-Shampoo, and recent hybrids including SOAP and SPlus, all emerge as special cases of the same principle. Within this framework, we provide the first systematic treatment of affine and scale invariance in the matrix-parameterized setting, establishing necessary and sufficient conditions under generalized norms. Building on this foundation, we introduce two new methods, MuAdam and MuAdam-SANIA, which combine the spectral geometry of Muon with Adam-style preconditioning. Our experiments demonstrate that these optimizers are competitive with, and in some cases outperform, existing state-of-the-art methods. Our code is available at this https URL
While traditional Deep Learning (DL) optimization methods treat all training samples equally, Distributionally Robust Optimization (DRO) adaptively assigns importance weights to different samples. However, a significant gap exists between DRO and current DL practices. Modern DL optimizers require adaptivity and the ability to handle stochastic gradients, as these methods demonstrate superior performance. Additionally, for practical applications, a method should allow weight assignment not only to individual samples, but also to groups of objects (for example, all samples of the same class). This paper aims to bridge this gap by introducing ALSO \unicodex2013 Adaptive Loss Scaling Optimizer \unicodex2013 an adaptive algorithm for a modified DRO objective that can handle weight assignment to sample groups. We prove the convergence of our proposed algorithm for non-convex objectives, which is the typical case for DL models. Empirical evaluation across diverse Deep Learning tasks, from Tabular DL to Split Learning tasks, demonstrates that ALSO outperforms both traditional optimizers and existing DRO methods.
An object-centric framework leveraging self-supervised pretraining improves Latent Action Policy Optimization (LAPO) by disentangling task-relevant dynamics from visual distractors. This approach mitigates the negative effects of distractors by an average of 50% in downstream task performance on Distracting Control Suite and Distracting MetaWorld benchmarks.
This research provides a comprehensive review and taxonomy of reward engineering and shaping techniques in Reinforcement Learning (RL). It systematically categorizes methods for designing and refining reward functions, demonstrating how these approaches accelerate learning, improve exploration, and enhance robustness across various RL applications.
New methods, Belief-FB (BFB) and Rotation-FB (RFB), allow Behavioral Foundation Models (BFMs) to adapt to different environmental dynamics without additional training. These approaches, which explicitly model dynamics belief and disentangle policy representations, consistently outperform existing baselines on tasks like Randomized FourRooms, PointMass, and AntWind, demonstrating improved zero-shot generalization.
27 Sep 2025
Physics-informed neural networks (PINNs) have gained prominence in recent years and are now effectively used in a number of applications. However, their performance remains unstable due to the complex landscape of the loss function. To address this issue, we reformulate PINN training as a nonconvex-strongly concave saddle-point problem. After establishing the theoretical foundation for this approach, we conduct an extensive experimental study, evaluating its effectiveness across various tasks and architectures. Our results demonstrate that the proposed method outperforms the current state-of-the-art techniques.
Researchers at the Artificial Intelligence Research Institute (AIRI) demonstrate that explicitly incorporating reinforcement learning objectives into offline in-context reinforcement learning (ICRL) models enhances performance. Their methods achieved approximately 30% average performance improvement over Algorithm Distillation (AD) across over 150 diverse datasets, and doubled performance in complex environments like XLand-MiniGrid.
The widespread utilization of language models in modern applications is inconceivable without Parameter-Efficient Fine-Tuning techniques, such as low-rank adaptation (LoRA), which adds trainable adapters to selected layers. Although LoRA may obtain accurate solutions, it requires significant memory to train large models and intuition on which layers to add adapters. In this paper, we propose a novel method, WeightLoRA, which overcomes this issue by adaptive selection of the most critical LoRA heads throughout the optimization process. As a result, we can significantly reduce the number of trainable parameters while maintaining the capability to obtain consistent or even superior metric values. We conduct experiments for a series of competitive benchmarks and DeBERTa, BART, and Llama models, comparing our method with different adaptive approaches. The experimental results demonstrate the efficacy of WeightLoRA and the superior performance of WeightLoRA+ in almost all cases.
We propose a novel architecture and method of explainable classification with
Concept Bottleneck Models (CBMs). While SOTA approaches to Image Classification
task work as a black box, there is a growing demand for models that would
provide interpreted results. Such a models often learn to predict the
distribution over class labels using additional description of this target
instances, called concepts. However, existing Bottleneck methods have a number
of limitations: their accuracy is lower than that of a standard model and CBMs
require an additional set of concepts to leverage. We provide a framework for
creating Concept Bottleneck Model from pre-trained multi-modal encoder and new
CLIP-like architectures. By introducing a new type of layers known as Concept
Bottleneck Layers, we outline three methods for training them: with
ℓ1-loss, contrastive loss and loss function based on Gumbel-Softmax
distribution (Sparse-CBM), while final FC layer is still trained with
Cross-Entropy. We show a significant increase in accuracy using sparse hidden
layers in CLIP-based bottleneck models. Which means that sparse representation
of concepts activation vector is meaningful in Concept Bottleneck Models.
Moreover, with our Concept Matrix Search algorithm we can improve CLIP
predictions on complex datasets without any additional training or fine-tuning.
The code is available at: this https URL
A study from Innopolis University and HSE University systematically analyzed the relationship between brain hemisphere states and EEG frequency bands, utilizing optimized deep learning models and SHAP for interpretability, achieving high classification precision (up to 0.95 ROC AUC) in distinguishing hemispheric activity during visual perception.
SAGE introduces a two-phase, streaming, and memory-efficient method for selecting representative data subsets for neural network training, utilizing Frequent Directions sketching and agreement-driven gradient scoring. It achieves 3-6x training speed-ups and reduced memory usage while maintaining or surpassing full-data accuracy on various benchmarks, even with aggressive data pruning of up to 75%.
In recent years, non-convex optimization problems are more often described by
generalized (L0,L1)-smoothness assumption rather than standard one.
Meanwhile, severely corrupted data used in these problems has increased the
demand for methods capable of handling heavy-tailed noises, i.e., noises with
bounded κ-th moment. Motivated by these real-world trends and
challenges, we explore sign-based methods in this setup and demonstrate their
effectiveness in comparison with other popular solutions like clipping or
normalization.
In theory, we prove the first-known high probability convergence bounds under
(L0,L1)-smoothness and heavy-tailed noises with mild parameter
dependencies. In the case of standard smoothness, these bounds are novel for
sign-based methods as well. In particular, SignSGD with batching achieves
sample complexity $\tilde{O}\left(\left(\frac{\Delta L_0d}{\varepsilon^2} +
\frac{\Delta L_1d^\frac{3}{2}}{\varepsilon}\right)\left[1 +
\left(\frac{\sigma}{\varepsilon}\right)^\frac{\kappa}{\kappa-1}\right]\right),
\kappa \in (1,2]$. Under the assumption of symmetric noises, SignSGD with
Majority Voting can robustly work on the whole range of κ∈(0,2] with
complexity $\tilde{O}\left(\left(\frac{\Delta L_0d}{\varepsilon^2} +
\frac{\Delta L_1d^\frac{3}{2}}{\varepsilon}\right)\left[\frac{1}{\kappa^2} +
\frac{\sigma^2}{\varepsilon^2}\right]\right)$. We also obtain results for
parameter-agnostic setups, Polyak-Lojasiewicz functions and momentum-based
methods (in expectation). Our theoretical findings are supported by the
superior performance of sign-based methods in training Large Language Models
compared to clipping and normalization.
There are no more papers matching your filters at the moment.