Large Language Models (LLMs) have revolutionized natural language processing, but their varying capabilities and costs pose challenges in practical applications. LLM routing addresses this by dynamically selecting the most suitable LLM for each query/task. Previous approaches treat this as a supervised learning problem, assuming complete knowledge of optimal query-LLM pairings. However, real-world scenarios lack such comprehensive mappings and face evolving user queries. We thus propose to study LLM routing as a contextual bandit problem, enabling adaptive decision-making using bandit feedback without requiring exhaustive inference across all LLMs for all queries (in contrast to supervised routing). To address this problem, we develop a shared embedding space for queries and LLMs, where query and LLM embeddings are aligned to reflect their affinity. This space is initially learned from offline human preference data and refined through online bandit feedback. We instantiate this idea through Preference-prior Informed Linucb fOr adaptive rouTing (PILOT), a novel extension of LinUCB. To handle diverse user budgets for model routing, we introduce an online cost policy modeled as a multi-choice knapsack problem, ensuring resource-efficient routing.

Training large language models (LLMs) typically involves pre-training on massive corpora, only to restart the process entirely when new data becomes available. A more efficient and resource-conserving approach would be continual pre-training, where models are updated with new data rather than retraining from scratch. However, the introduction of new data often causes distribution shifts, leading to performance degradation on previously learned tasks. In this paper, we take a deeper look at two popular proposals for addressing this distribution shift within the continual learning literature: experience replay and gradient alignment. We consider continual pre-training of models within the Llama family of architectures at a large scale across languages with 100 billion tokens of training data in each language, finding that both replay and gradient alignment lead to more stable learning without forgetting. This conclusion holds both as we vary the model scale and as we vary the number and diversity of tasks. Moreover, we are the first to demonstrate the effectiveness of gradient alignment techniques in the context of LLM pre-training and propose an efficient implementation of meta-experience replay (MER) that imbues experience replay with the benefits of gradient alignment despite negligible compute and memory overhead. Our scaling analysis across model sizes and replay rates indicates that small rates of replaying old examples are definitely a more valuable use of compute than investing in model size, but that it is more compute efficient to scale the size of the model than invest in high rates of replaying old examples.

With the increasing complexity of video data and the need for more efficient long-term temporal understanding, existing long-term video understanding methods often fail to accurately capture and analyze extended video sequences. These methods typically struggle to maintain performance over longer durations and to handle the intricate dependencies within the video content. To address these limitations, we propose a simple yet effective large multi-modal model framework for long-term video understanding that incorporates a novel visual compressor, the In-context, Question Adaptive Visual Compressor (IQViC). The key idea, inspired by humans' selective attention and in-context memory mechanisms, is to introduce a novel visual compressor and incorporate efficient memory management techniques to enhance long-term video question answering. Our framework utilizes IQViC, a transformer-based visual compressor, enabling question-conditioned in-context compression, unlike existing methods that rely on full video visual features. This selectively extracts relevant information, significantly reducing memory token requirements. Through extensive experiments on a new dataset based on InfiniBench for long-term video understanding, and standard benchmarks used for existing methods' evaluation, we demonstrate the effectiveness of our proposed IQViC framework and its superiority over state-of-the-art methods in terms of video understanding accuracy and memory efficiency.

The SoccerNet 2022 challenges were the second annual video understanding challenges organized by the SoccerNet team. In 2022, the challenges were composed of 6 vision-based tasks: (1) action spotting, focusing on retrieving action timestamps in long untrimmed videos, (2) replay grounding, focusing on retrieving the live moment of an action shown in a replay, (3) pitch localization, focusing on detecting line and goal part elements, (4) camera calibration, dedicated to retrieving the intrinsic and extrinsic camera parameters, (5) player re-identification, focusing on retrieving the same players across multiple views, and (6) multiple object tracking, focusing on tracking players and the ball through unedited video streams. Compared to last year's challenges, tasks (1-2) had their evaluation metrics redefined to consider tighter temporal accuracies, and tasks (3-6) were novel, including their underlying data and annotations. More information on the tasks, challenges and leaderboards are available on this https URL. Baselines and development kits are available on this https URL.

The quantum transduction, or equivalently quantum frequency conversion, is vital for the realization of, e.g., quantum networks, distributed quantum computing, and quantum repeaters. The microwave-to-optical quantum transduction is of particular interest in the field of superconducting quantum computing, since interconnecting dilution refrigerators is considered inevitable for realizing large-scale quantum computers with fault-tolerance. In this review, we overview recent theoretical and experimental studies on the quantum transduction between microwave and optical photons. We describe a generic theory for the quantum transduction employing the input-output formalism, from which the essential quantities characterizing the transduction, i.e., the expressions for the transduction efficiency, the added noise, and the transduction bandwidth are derived. We review the major transduction methods that have been experimentally demonstrated, focusing the transduction via the optomechanical effect, the electro-optic effect, the magneto-optic effect, and the atomic ensembles. We also briefly review the recent experimental progress on the quantum transduction from superconducting qubit to optical photon, which is an important step toward the quantum state transfer between distant superconducting qubits interconnected over optical fibers.

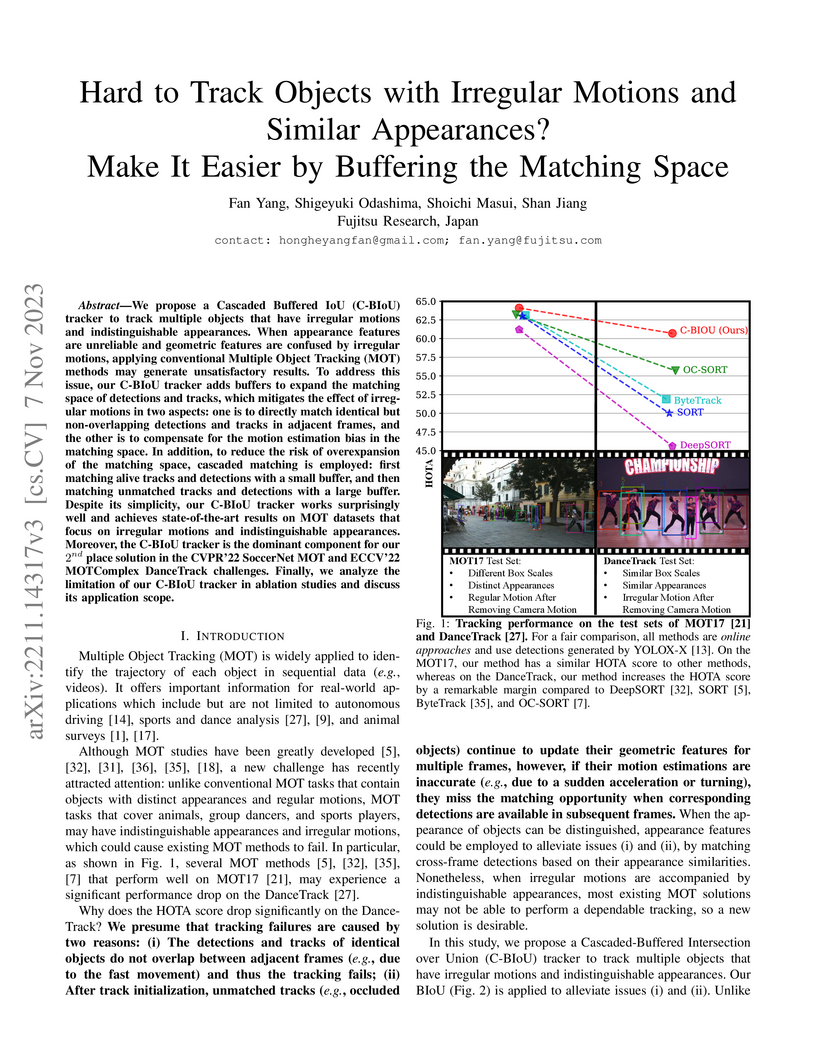
We propose a Cascaded Buffered IoU (C-BIoU) tracker to track multiple objects that have irregular motions and indistinguishable appearances. When appearance features are unreliable and geometric features are confused by irregular motions, applying conventional Multiple Object Tracking (MOT) methods may generate unsatisfactory results. To address this issue, our C-BIoU tracker adds buffers to expand the matching space of detections and tracks, which mitigates the effect of irregular motions in two aspects: one is to directly match identical but non-overlapping detections and tracks in adjacent frames, and the other is to compensate for the motion estimation bias in the matching space. In addition, to reduce the risk of overexpansion of the matching space, cascaded matching is employed: first matching alive tracks and detections with a small buffer, and then matching unmatched tracks and detections with a large buffer. Despite its simplicity, our C-BIoU tracker works surprisingly well and achieves state-of-the-art results on MOT datasets that focus on irregular motions and indistinguishable appearances. Moreover, the C-BIoU tracker is the dominant component for our 2-nd place solution in the CVPR'22 SoccerNet MOT and ECCV'22 MOTComplex DanceTrack challenges. Finally, we analyze the limitation of our C-BIoU tracker in ablation studies and discuss its application scope.

Although there is a significant development in 3D Multi-view Multi-person Tracking (3D MM-Tracking), current 3D MM-Tracking frameworks are designed separately for footprint and pose tracking. Specifically, frameworks designed for footprint tracking cannot be utilized in 3D pose tracking, because they directly obtain 3D positions on the ground plane with a homography projection, which is inapplicable to 3D poses above the ground. In contrast, frameworks designed for pose tracking generally isolate multi-view and multi-frame associations and may not be robust to footprint tracking, since footprint tracking utilizes fewer key points than pose tracking, which weakens multi-view association cues in a single frame. This study presents a Unified Multi-view Multi-person Tracking framework to bridge the gap between footprint tracking and pose tracking. Without additional modifications, the framework can adopt monocular 2D bounding boxes and 2D poses as the input to produce robust 3D trajectories for multiple persons. Importantly, multi-frame and multi-view information are jointly employed to improve the performance of association and triangulation. The effectiveness of our framework is verified by accomplishing state-of-the-art performance on the Campus and Shelf datasets for 3D pose tracking, and by comparable results on the WILDTRACK and MMPTRACK datasets for 3D footprint tracking.

Learning high-dimensional distributions is a significant challenge in machine learning and statistics. Classical research has mostly concentrated on asymptotic analysis of such data under suitable assumptions. While existing works [Bhattacharyya et al.: SICOMP 2023, Daskalakis et al.: STOC 2021, Choo et al.: ALT 2024] focus on discrete distributions, the current work addresses the tree structure learning problem for Gaussian distributions, providing efficient algorithms with solid theoretical guarantees. This is crucial as real-world distributions are often continuous and differ from the discrete scenarios studied in prior works. In this work, we design a conditional mutual information tester for Gaussian random variables that can test whether two Gaussian random variables are independent, or their conditional mutual information is at least $\varepsilon$, for some parameter $\varepsilon \in (0,1)$ using $\mathcal{O}(\varepsilon^{-1})$ samples which we show to be near-optimal. In contrast, an additive estimation would require $\Omega(\varepsilon^{-2})$ samples. Our upper bound technique uses linear regression on a pair of suitably transformed random variables. Importantly, we show that the chain rule of conditional mutual information continues to hold for the estimated (conditional) mutual information. As an application of such a mutual information tester, we give an efficient $\varepsilon$-approximate structure-learning algorithm for an $n$-variate Gaussian tree model that takes $\widetilde{\Theta}(n\varepsilon^{-1})$ samples which we again show to be near-optimal. In contrast, when the underlying Gaussian model is not known to be tree-structured, we show that $\widetilde{\Theta}(n^2\varepsilon^{-2})$ samples are necessary and sufficient to output an $\varepsilon$-approximate tree structure. We perform extensive experiments that corroborate our theoretical convergence bounds.

Quantum machine learning models that leverage quantum circuits as quantum feature maps (QFMs) are recognized for their enhanced expressive power in learning tasks. Such models have demonstrated rigorous end-to-end quantum speedups for specific families of classification problems. However, deploying deep QFMs on real quantum hardware remains challenging due to circuit noise and hardware constraints. Additionally, variational quantum algorithms often suffer from computational bottlenecks, particularly in accurate gradient estimation, which significantly increases quantum resource demands during training. We propose Iterative Quantum Feature Maps (IQFMs), a hybrid quantum-classical framework that constructs a deep architecture by iteratively connecting shallow QFMs with classically computed augmentation weights. By incorporating contrastive learning and a layer-wise training mechanism, the IQFMs framework effectively reduces quantum runtime and mitigates noise-induced degradation. In tasks involving noisy quantum data, numerical experiments show that the IQFMs framework outperforms quantum convolutional neural networks, without requiring the optimization of variational quantum parameters. Even for a typical classical image classification benchmark, a carefully designed IQFMs framework achieves performance comparable to that of classical neural networks. This framework presents a promising path to address current limitations and harness the full potential of quantum-enhanced machine learning.

One-time programs (Goldwasser, Kalai and Rothblum, CRYPTO 2008) are functions that can be run on any single input of a user's choice, but not on a second input. Classically, they are unachievable without trusted hardware, but the destructive nature of quantum measurements seems to provide a quantum path to constructing them. Unfortunately, Broadbent, Gutoski and Stebila showed that even with quantum techniques, a strong notion of one-time programs, similar to ideal obfuscation, cannot be achieved for any non-trivial quantum function. On the positive side, Ben-David and Sattath (Quantum, 2023) showed how to construct a one-time program for a certain (probabilistic) digital signature scheme, under a weaker notion of one-time program security. There is a vast gap between achievable and provably impossible notions of one-time program security, and it is unclear what functionalities are one-time programmable under the achievable notions of security. In this work, we present new, meaningful, yet achievable definitions of one-time program security for probabilistic classical functions. We show how to construct one time programs satisfying these definitions for all functions in the classical oracle model and for constrained pseudorandom functions in the plain model. Finally, we examine the limits of these notions: we show a class of functions which cannot be one-time programmed in the plain model, as well as a class of functions which appears to be highly random given a single query, but whose one-time program form leaks the entire function even in the oracle model.

Secure key leasing allows a cryptographic key to be leased as a quantum state in such a way that the key can later be revoked in a verifiable manner. In this work, we propose a modular framework for constructing secure key leasing with a classical-lessor, where the lessor is entirely classical and, in particular, the quantum secret key can be both leased and revoked using only classical communication. Based on this framework, we obtain classical-lessor secure key leasing schemes for public-key encryption (PKE), pseudorandom function (PRF), and digital signature. We adopt the strong security notion known as security against verification key revealing attacks (VRA security) proposed by Kitagawa et al. (Eurocrypt 2025) into the classical-lessor setting, and we prove that all three of our schemes satisfy this notion under the learning with errors assumption. Our PKE scheme improves upon the previous construction by Goyal et al. (Eurocrypt 2025), and our PRF and digital signature schemes are respectively the first PRF and digital signature with classical-lessor secure key leasing property.

Quantum computers offer a promising route to tackling problems that are classically intractable such as in prime-factorization, solving large-scale linear algebra and simulating complex quantum systems, but potentially require fault-tolerant quantum hardware. On the other hand, variational quantum algorithms (VQAs) are a promising approach for leveraging near-term quantum computers to solve complex problems. However, there remain major challenges in their trainability and resource costs on quantum hardware. Here we address these challenges by adopting Hardware Efficient and dynamical LIe algebra supported Ansatz (HELIA), and propose two training methods that combine an existing classical-enhanced g-sim method and the quantum-based Parameter-Shift Rule (PSR). Our improvement comes from distributing the resources required for gradient estimation and training to both classical and quantum hardware. We numerically evaluate our approach for ground-state estimation of 6 to 18-qubit Hamiltonians using the Variational Quantum Eigensolver (VQE) and quantum phase classification for up to 12-qubit Hamiltonians using quantum neural networks. For VQE, our method achieves higher accuracy and success rates, with an average reduction in quantum hardware calls of up to 60% compared to purely quantum-based PSR. For classification, we observe test accuracy improvements of up to 2.8%. We also numerically demonstrate the capability of HELIA in mitigating barren plateaus, paving the way for training large-scale quantum models.

Fault localization (FL) is a critical step in debugging which typically relies on repeated executions to pinpoint faulty code regions. However, repeated executions can be impractical in the presence of non-deterministic failures or high execution costs. While recent efforts have leveraged Large Language Models (LLMs) to aid execution-free FL, these have primarily focused on identifying faults in the system under test (SUT) rather than in the often complex system test code. However, the latter is also important as, in practice, many failures are triggered by faulty test code. To overcome these challenges, we introduce a fully static, LLM-driven approach for system test code fault localization (TCFL) that does not require executing the test case. Our method uses a single failure execution log to estimate the test's execution trace through three novel algorithms that identify only code statements likely involved in the failure. This pruned trace, combined with the error message, is used to prompt the LLM to rank potential faulty locations. Our black-box, system-level approach requires no access to the SUT source code and is applicable to large test scripts that assess full system behavior. We evaluate our technique at function, block, and line levels using an industrial dataset of faulty test cases not previously used in pre-training LLMs. Results show that our best estimated trace closely match actual traces, with an F1 score of around 90%. Additionally, pruning the complex system test code reduces the LLM's inference time by up to 34% without any loss in FL performance. Our results further suggest that block-level TCFL offers a practical balance, narrowing the search space while preserving useful context, achieving an 81% hit rate at top-3 (Hit@3).

This is our 2nd-place solution for the ECCV 2022 Multiple People Tracking in Group Dance Challenge. Our method mainly includes two steps: online short-term tracking using our Cascaded Buffer-IoU (C-BIoU) Tracker, and, offline long-term tracking using appearance feature and hierarchical clustering. Our C-BIoU tracker adds buffers to expand the matching space of detections and tracks, which mitigates the effect of irregular motions in two aspects: one is to directly match identical but non-overlapping detections and tracks in adjacent frames, and the other is to compensate for the motion estimation bias in the matching space. In addition, to reduce the risk of overexpansion of the matching space, cascaded matching is employed: first matching alive tracks and detections with a small buffer, and then matching unmatched tracks and detections with a large buffer. After using our C-BIoU for online tracking, we applied the offline refinement introduced by ReMOTS.

We present a robust multi-camera gymnast tracking, which has been applied at international gymnastics championships for gymnastics judging. Despite considerable progress in multi-camera tracking algorithms, tracking gymnasts presents unique challenges: (i) due to space restrictions, only a limited number of cameras can be installed in the gymnastics stadium; and (ii) due to variations in lighting, background, uniforms, and occlusions, multi-camera gymnast detection may fail in certain views and only provide valid detections from two opposing views. These factors complicate the accurate determination of a gymnast's 3D trajectory using conventional multi-camera triangulation. To alleviate this issue, we incorporate gymnastics domain knowledge into our tracking solution. Given that a gymnast's 3D center typically lies within a predefined vertical plane during \revised{much of their} performance, we can apply a ray-plane intersection to generate coplanar 3D trajectory candidates for opposing-view detections. More specifically, we propose a novel cascaded data association (DA) paradigm that employs triangulation to generate 3D trajectory candidates when cross-view detections are sufficient, and resort to the ray-plane intersection when they are insufficient. Consequently, coplanar candidates are used to compensate for uncertain trajectories, thereby minimizing tracking failures. The robustness of our method is validated through extensive experimentation, demonstrating its superiority over existing methods in challenging scenarios. Furthermore, our gymnastics judging system, equipped with this tracking method, has been successfully applied to recent Gymnastics World Championships, earning significant recognition from the International Gymnastics Federation.

Zero-Knowledge (ZK) protocols have been intensely studied due to their fundamental importance and versatility. However, quantum information's inherent differences significantly alter the landscape, necessitating a re-examination of ZK designs. A crucial aspect is round complexity, linked to $\textit{simulation}$, which forms the foundation of ZK definition and security proofs. In the $\textit{post-quantum}$ setting, where honest parties and channels are classical but adversaries quantum, Chia et al. [FOCS'21] showed constant-round $\textit{black-box-simulatable}$ ZK arguments (BBZK) for $\mathbf{NP}$ are impossible unless $\mathbf{NP} \subseteq \mathbf{BQP}$. But this problem remains open when all parties and communication are quantum. Indeed, this problem interests the broader theory of quantum computing. Investigating how quantum power alters tasks like the $\textit{unconditional}$ security of QKD and incorporating OT in MiniQCrypt has been crucial. Moreover, quantum communication has enabled round compression for commitments and interactive arguments. Along this line, understanding if quantum computing could fundamentally change ZK protocols is vital. We resolved this problem by proving that only languages in $\mathbf{BQP}$ admit constant-round $\textit{fully-quantum}$ BBZK. This result holds significant implications. Firstly, it illuminates the nature of quantum zero-knowledge and provides valuable insights for designing future protocols in the quantum realm. Secondly, it relates ZK round complexity with the intriguing problem of $\mathbf{BQP}$ vs $\mathbf{QMA}$, which is out of the reach of previous analogue impossibility results in the classical or post-quantum setting. Lastly, it justifies the need for the $\textit{non-black-box}$ simulation techniques or the relaxed security notions employed in existing constant-round fully-quantum BBZK protocols.